Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

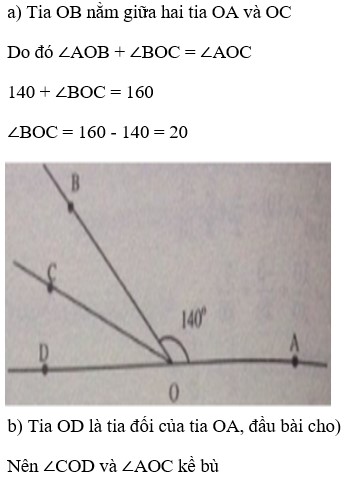
a) Tia OB nằm giữa hai tia OA và OC
Do đó A O B ^ + B O C ^ = A O C ^
140 + B O C ^ = 160
B O C ^ = 160 - 140 = 20
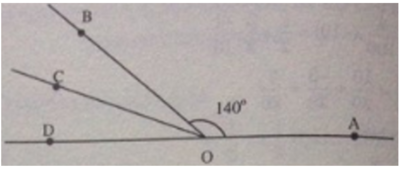
b) Tia OD là tia đối của tia OA, đầu bài cho)
Nên C O D ^ v à A O C ^ kề bù
Ta có C O D ^ + A O C ^ = 180 0
C O D ^ + 160 0 = 180 0
C O D ^ = 180 0 - 160 0 = 20 0
c) Ta có tia OC nằm gữa hai tia OB và OD (1)
Mặt khác C O D ^ = B O C ^ ( =20)(2)
Từ (1) và (2) ta có tia OC là tia phân giác của góc BOD

\(\widehat{AOB}\)= \(140^o\)
\(\widehat{AOC}\)= \(160^o\)
Nên để tính góc \(\widehat{BOC}\)ta lấy
\(\widehat{AOC}\)- \(\widehat{AOB}\) = \(160^o\)- \(140^o\) = \(20^o\)
\(\widehat{BOC}\) = \(20^o\)
Góc COD :
AOD đối nhau nên góc \(\widehat{AOD}\)= \(180^o\)
Rồi ta lấy góc \(\widehat{AOD}\)- \(\widehat{AOC}\)= \(180^o\) - \(160^o\) = \(20^o\)
\(\widehat{COD}\) = \(20^o\)
Tia OC là tia phân giác của góc \(\widehat{BOD}\)
VÌ tia OC nằm giữa góc \(\widehat{BOD}\)
CHÚC BẠN THÀNH CÔNG

a) Tia OB nằm giữa hai tia OA và OC
Do đó ∠AOB + ∠BOC = ∠AOC
140 + ∠BOC = 160
∠BOC = 160 - 140 = 20
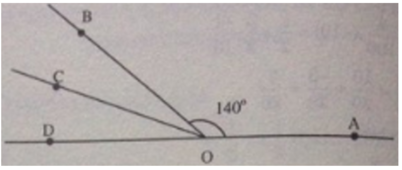

c) Ta có tia OC nằm gữa hai tia OB và OD (1)
Mặt khác ∠COD = ∠BOC( =20)(2)
Từ (1) và (2) ta có tia OC là tia phân giác của góc BOD

a, vì trên cùng nửa mặt phẳng bờ chứa tia oa có tia AOB = \(70^0\) <AOC =\(140^0\)
=> tia OB nằm giữa tia OC và OA
b, ta có BOA + BOC =COA
\(70^0\)+BOC =\(140^0\)
BOC = \(140^0-70^0\)
BOC = \(70^0\)
Vậy BOC = \(70^0\)
c, vì BOC =BOA =\(\frac{COA}{2}\)( =\(70^0\))
=>Tia OB là tia phân giác góc COA
a/Trên nửa mặt phẳng bờ chứa tia OA,ta có góc AOB= 70 độ < góc AOC= 140 độ
Vậy tia OB nằm giữa 2 tia OC và OA
b/Vì tia OB nằm giữa hai tia OC và OA nên
Ta có: góc AOB+góc BOC = góc AOC
Thay số: 70 độ + góc BOC =140 độ
Suy ra góc BOC = 140 độ - 70 độ = 70 độ
Vậy góc BOC = 70 độ
c/Tia OB là tia phân giác của góc AOC vì
+Tia OB nằm giữa hai tia OA và OC ( theo a)
+góc AOB = góc BOC = 70 độ (theo b)
d/Vì góc DOB là góc bẹt nên góc DOB = 180 độ

Giải chi tiết:
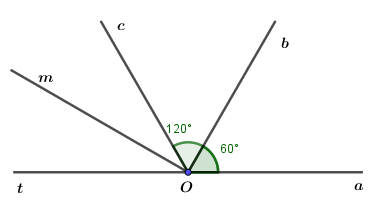
a) Trên cùng một nửa mặt phẳng bờ chứa tia OaOa, ta có ˆaOb<ˆaOc(600<1200)aOb^<aOc^(600<1200)nên ObOb là tia nằm giữa hai tia OaOa và OcOc
⇒ˆaOb+ˆbOc=ˆaOc⇒ˆbOc=ˆaOc−ˆaOb=1200−600=600⇒aOb^+bOc^=aOc^⇒bOc^=aOc^−aOb^=1200−600=600.
b) Theo chứng minh trên ta có tia ObOb là tia nằm giữa hai tia OaOa và OcOc.
Lại có ˆaOb=ˆaOc=600aOb^=aOc^=600
Suy ra ObOb là tia phân giác của ˆaOcaOc^.
c) Vì tia OtOt là tia đối của tia OaOa nên góc aOtaOt là góc bẹt, hay ˆaOt=1800aOt^=1800.
Trên cùng một nửa mặt phẳng bờ chứa tia OaOa, ta có ˆaOc<ˆaOt(1200<1800)aOc^<aOt^(1200<1800)nên OcOc là tia nằm giữa hai tia OaOa và OtOt
⇒ˆaOc+ˆcOt=ˆaOt⇒ˆcOt=ˆaOt−ˆaOc=1800−1200=600⇒aOc^+cOt^=aOt^⇒cOt^=aOt^−aOc^=1800−1200=600.
Vì OmOm là tia phân giác của ˆcOtcOt^ nên ˆcOm=12ˆcOt=6002=300cOm^=12cOt^=6002=300.
Ta có ˆbOc+ˆcOm=600+300=900bOc^+cOm^=600+300=900, do đó ˆbOcbOc^ và ˆcOmcOm^ là hai góc phụ nhau.
Chọn D

a: Trên cùng một nửa mặt phẳng bờ chứa tia Oa, ta có: \(\widehat{aOb}< \widehat{aOc}\)
nên tia Ob nằm giữa hai tia Oa và Oc
Suy ra: \(\widehat{aOb}+\widehat{bOc}=\widehat{aOc}\)
hay \(\widehat{bOc}=70^0\)

Tự vẽ hình nhé!
a, Trên cùng một nửa mặt phẳng bờ chứa tia OA ta có : AOC<AOB (50<100) nên tia Oc nằm giữa 2 tia Oa Và Ob
b, Vì tia Oc nằm giữa Oa và Ob (1)
nên ta có: aOb - aOc = cOb
100 - 50 = cOb
50 = cOb
Vậy cOb = 50 độ
Vì aOc=50 và cOb=50 nên aOc = cOb (2)
Từ (1) và (2) suy ra Oc là tia phân giác của aOb
c, ....................................................................................

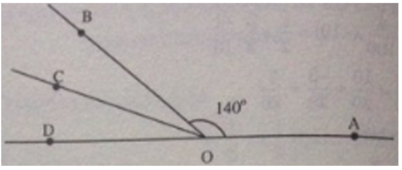
b) Tia OD là tia đối của tia OA, đầu bài cho)
Nên ∠COD và ∠AOC kề bù
Ta có ∠COD + ∠AOC = 180 0
∠COD + 160 0 = 180 0
∠COD = 180 0 - 160 0 = 20 0