Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo em ý kiến của bạn Nam là đúng.
Ta có: Hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0}\) nên \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Hàm số \(y = g\left( x \right)\) không liên tục tại \({x_0}\) nên \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) \ne g\left( {{x_0}} \right)\)
Do đó \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) + \mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) \ne f\left( {{x_0}} \right) + g\left( {{x_0}} \right)\)
Vì vậy hàm số không liên tục tại x0.

a) Ta có  = 22 +2.2 +4 = 12.
= 22 +2.2 +4 = 12.
Vì ![]() nên hàm số y = g(x) gián đoạn tại x0 = 2.
nên hàm số y = g(x) gián đoạn tại x0 = 2.
b) Để hàm số y = f(x) liên tục tại x0 = 2 thì ta cần thay số 5 bởi số 12

a) Ta có \(f\left( {{x_0}} \right) = {x_0} + 1;\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {x + 1} \right) = \mathop {\lim }\limits_{x \to {x_0}} x + 1 = {x_0} + 1\)
\( \Rightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Vậy hàm số \(f\left( x \right)\) liên tục tại \({x_0}.\)
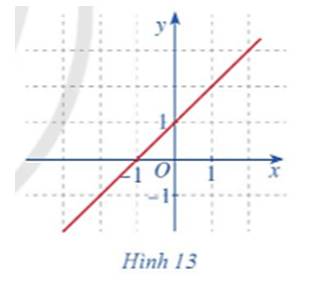
b) Dựa vào đồ thị hàm số ta thấy: Đồ thị hàm số là một đường thẳng liền mạch với mọi giá trị \(x \in \mathbb{R}.\)

Theo định nghĩa ta có :
\(f'\left(x\right)=\lim\limits_{\Delta x\rightarrow0}\frac{f\left(a+\right)-f\left(a\right)}{\Delta x}\)
\(=\lim\limits_{\Delta x\rightarrow0}\frac{\left(a+\Delta x-1\right)\varphi\left(a+\Delta x\right)}{\Delta x}\) do (\(f\left(a\right)=0\))
\(=\lim\limits_{\Delta x\rightarrow0}\varphi\left(a+\Delta x\right)\)
Khi \(\Delta x\rightarrow0\) thì \(a+\Delta x\rightarrow a\) và do \(\varphi\left(x\right)\) là hàm liên tục tại x = a nên có :
\(\lim\limits_{\Delta x\rightarrow0}\varphi\left(a+\Delta x\right)=\varphi\left(a\right)\)
Vậy \(f'\left(a\right)=\varphi\left(a\right)\)

\(\lim\limits_{x\rightarrow0}\left|f\left(x\right)\right|=\lim\limits_{x\rightarrow0}\left|x^2sin\dfrac{1}{x}\right|< \lim\limits_{x\rightarrow0}\left|x^2\right|=0\).
Vậy \(\lim\limits_{x\rightarrow0}f\left(x\right)=0\).
\(f\left(0\right)=A\).
Để hàm số liên tục tại \(x=0\) thì \(\lim\limits_{x\rightarrow0}f\left(x\right)=f\left(0\right)\Leftrightarrow A=0\).
Để xét hàm số có đạo hàm tại \(x=0\) ta xét giới hạn:
\(\lim\limits_{x\rightarrow0}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0}\dfrac{x^2sin\dfrac{1}{x}}{x}=\lim\limits_{x\rightarrow0}xsin\dfrac{1}{x}=0\).
Vậy hàm số có đạo hàm tại \(x=0\).



Ý kiến đúng
Giả sử ngược lại y = f(x) + g(x) liên tục tại x0. Đặt h(x) = f(x) + g(x). Ta có g(x) = h(x) – f(x).
Vì y = h(x) và y = f(x) liên tục tại x0 nên hiệu của chúng là hàm số y = g(x) phải liên tục tại x0. Điều này trái với giả thiết là y = g(x) không liên tục tại x0.