Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hàm số \(y=\sin x\) giảm trên đoạn \(\left[\dfrac{\pi}{2};\dfrac{3\pi}{2}\right]\) và tăng trên đoạn \(\left[\dfrac{3\pi}{2};2\pi\right]\)
b) \(y=\sin x\) giảm trên \(\left[-\pi;-\dfrac{\pi}{2}\right]\), tăng trên \(\left[-\dfrac{\pi}{2};0\right]\)
c) \(y=\sin x\) tăng trên \(\left[-2\pi;-\dfrac{3\pi}{2}\right]\), giảm trên \(\left[-\dfrac{3\pi}{2};-\pi\right]\)

a) y = sinx
- Khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
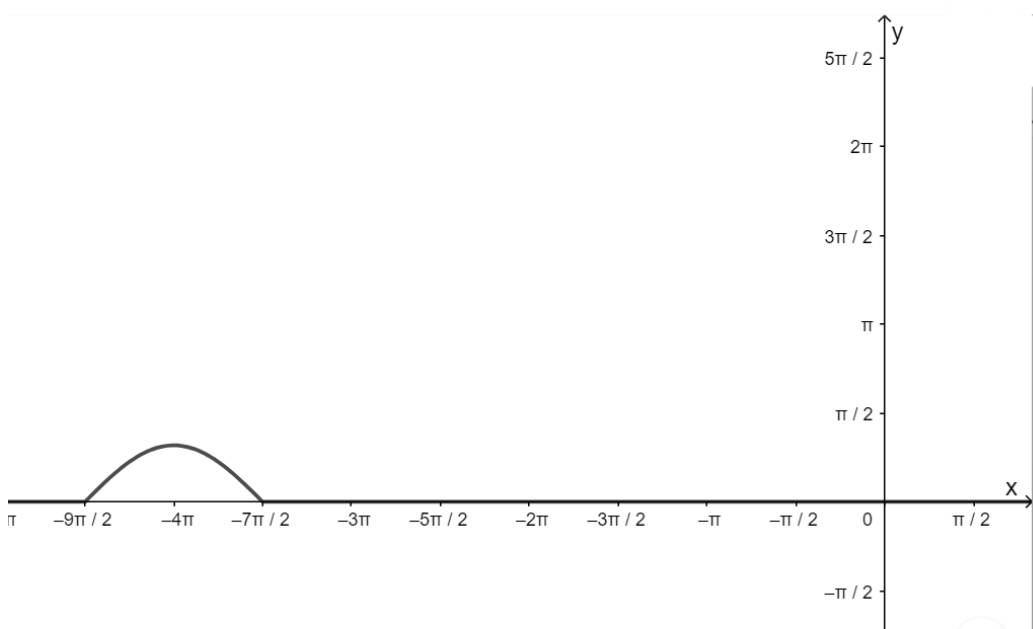
+ Đồng biến trên khoảng \(\left( { - \frac{{9\pi }}{2}; - 4\pi } \right)\)
+ Nghịch biến trên khoảng; \(\left( { - 4\pi ; - \frac{{7\pi }}{2}} \right)\)
- Khoảng \(\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
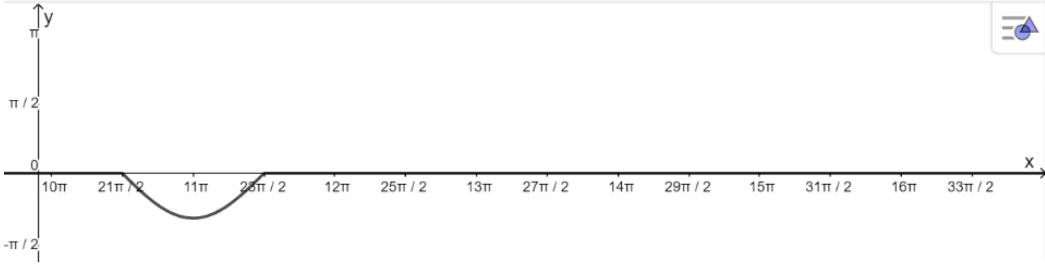
+ Đồng biến trên khoảng: \(\left( {11\pi ;\frac{{23\pi }}{2}} \right)\)
+ Nghịch biến trên khoảng: \(\left( {\frac{{21\pi }}{2};11\pi } \right)\)
\(y'=-2cos2x=0\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}\\x=\dfrac{\pi}{4}\end{matrix}\right.\)
BBT:
x y' y -pi/2 -pi/4 pi/4 pi/2 0 0 + - -
Hàm đồng biến trên \(\left(-\dfrac{\pi}{4};\dfrac{\pi}{4}\right)\) và nghịch biến trên các khoảng \(\left(-\dfrac{\pi}{2};-\dfrac{\pi}{4}\right);\left(\dfrac{\pi}{4};\dfrac{\pi}{2}\right)\)
nghịch biến đâu bạn