LN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HD
1
17 tháng 12 2016
Điểm cực tiểu A(0;-2), điểm cực đại B(2;2)
Mình không hiểu đề bài yêu cầu tìm đường thẳng đi qua điểm A và B, đi qua cả A và B hay là các tiếp tuyến tại A và B?
TN
1
HN
20 tháng 10 2021
Tập xác định: D=\(\left[-2\sqrt{2};2\sqrt{2}\right]\).
\(y'=1-\dfrac{x}{\sqrt{8-x^2}}\) = 0 \(\Rightarrow\) x=2.
Bảng biến thiên:
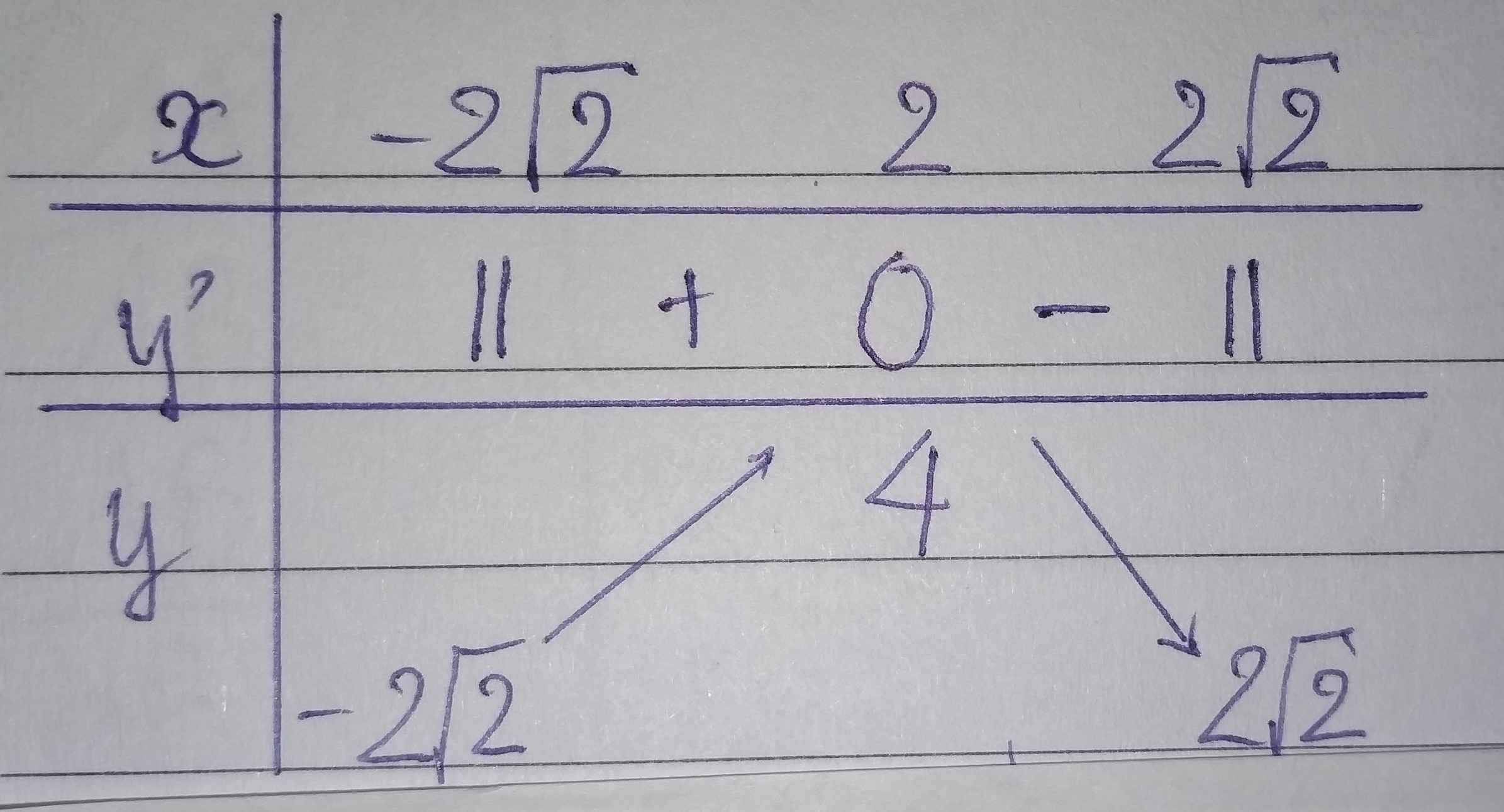
Vậy hàm số đã cho đồng biến trên khoảng (\(-2\sqrt{2}\);2), nghịch biến trên khoảng (2;\(2\sqrt{2}\)) và yCĐ=4 (tại x=2).
Tham khảo: Đồ thị:
LN
1
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 9 2021
a. ĐKXĐ: \(-3\le x\le3\)
\(y'=1-\dfrac{x}{\sqrt{9-x^2}}=\dfrac{\sqrt{9-x^2}-x}{\sqrt{9-x^2}}=0\Rightarrow x=\dfrac{3\sqrt{2}}{2}\)
Dấu của y':
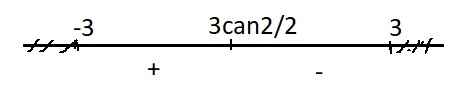
Hàm đồng biến trên \(\left(-3;\dfrac{3\sqrt{2}}{2}\right)\) và nghịch biến trên \(\left(\dfrac{3\sqrt{2}}{2};3\right)\)
b.
ĐKXĐ: \(x\ne2\)
\(y'=\dfrac{\left(-2x-1\right)\left(x+2\right)+x^2+x+2}{\left(x+2\right)^2}=\dfrac{-x^2-4x}{\left(x+2\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
Dấu của y':
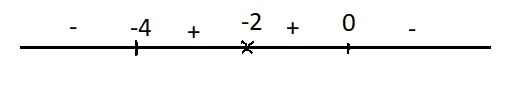
Hàm đồng biến trên các khoảng \(\left(-4;-2\right)\) và \(\left(-2;0\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-4\right)\) và \(\left(0;+\infty\right)\)
DD
Đoàn Đức Hà
Giáo viên
8 tháng 10 2021
\(y=x^3-mx^2+\left(1-2m\right)x+1\)
\(y'=3x^2-2mx+1-2m\)
Để đồ thị hàm số đã cho có hai cực trị nằm về hai phía của trục tung thì phương trình \(y'=0\)có hai nghiệm phân biệt \(x_1,x_2\)thỏa mãn \(x_1x_2< 0\).
Ta có: \(y'=0\Leftrightarrow3x^2-2mx+1-2m=0\)(1)
Để (1) có hai nghiệm phân biệt thỏa mãn \(x_1x_2< 0\)thì:
\(\hept{\begin{cases}\Delta'=m^2-3\left(1-2m\right)>0\\\frac{1-2m}{3}< 0\end{cases}}\Leftrightarrow m>\frac{1}{2}\).
Vậy \(m>\frac{1}{2}\)thỏa mãn ycbt.
11 tháng 7 2016
ta có y'=3x^2-m
để hs có cực trị thì y'=0 có nghiệm phân biệt <=>3x^2-m=0<=>x^2=m/3<=>m/3>0 =>m>0
vậy với m>0 thì hs có cực trị
2 tháng 4 2019
đáp án là :
Hàm số đã cho xác định trên D=R.
Tính y' = -3x2 + 12x - 9. Cho y' = 0 ⇔ -3x2 + 12x - 9 = 0 ⇔ 
Bảng biến thiên:
Dựa vào bảng biến thiên,hàm số đồng biến trên (1;3).
Hàm số nghịch biến trên các khoảng (-∞; 1) và (3; +∞)
2 tháng 4 2019
Hàm số đã cho xác định trên D=R.
Tính y' = -3x2 + 12x - 9. Cho y' = 0 ⇔ -3x2 + 12x - 9 = 0 ⇔
Bảng biến thiên:
Dựa vào bảng biến thiên,hàm số đồng biến trên (1;3).
Hàm số nghịch biến trên các khoảng (-∞; 1) và (3; +∞)
P/S : quá dễ , t là thần đồng mà .
Mỗi ngày 3 T i c k , giờ làm như lời hứa đi
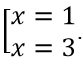
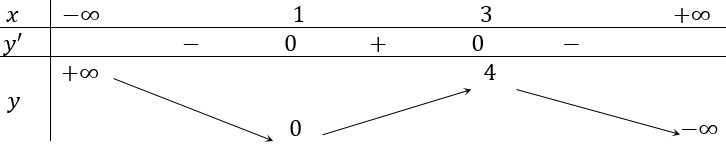
\(y'=-4x^3-4x=-4x\left(x^2+1\right)=0\Rightarrow x=0\)
Dấu của y':
Hàm đồng biến trên \(\left(-\infty;0\right)\) và nghịch biến trên \(\left(0;+\infty\right)\)
Qua \(x=0\) ta thấy y' đổi dấu từ dương sang âm nên \(x=0\) là điểm cực đại