Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Gọi M(x;y) là điểm biều diễn số phức z.
Từ giả thiết, ta có |z - 4 - 3i| =
5
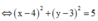
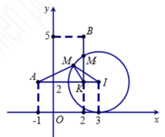
=> M thuộc đường tròn (C) tâm I(4;3), bán kính R = 5
Khi đó P = MA + MB với A(-1;3), B(1;-1)
Ta có 
Gọi E(0;1) là trung điểm của AB 
Do đó 
mà 
suy ra 
Với C là giao điểm của đường thẳng EI với đường tròn (C)
Vậy 
Dấu “=”xảy ra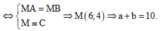 
Đáp án A.
Gọi M(x;y) là điểm biểu diễn số phức z.
Từ giả thiết, ta có 
=> M thuộc đường tròn (C) tâm I(4;3), bán kính R = 5
Khi đó P = MA + MB, với A(-1;3), B(1;-1)
Ta có
Gọi E(0;1) là trung điểm của AB
Do đó 
mà 
suy ra 
Với C là giao điểm của đường thẳng EI với đường tròn (C).
Vậy 
Dấu “=” xảy ra 
=> a + b = 10
Đáp án A.
Gọi M(x;y) là điểm biểu diễn số phức z.
Từ giả thiết, ta có 
=> M thuộc đường tròn (C) tâm I(4;3), bán kính R =
5
. Khi đó P = MA + MB, với A(-1;3), B(1;-1)
Ta có: 
Gọi E(0;1) là trung điểm của AB 
Do đó 
mà 
suy ra 
Với C là giao điểm của đường thẳng EI với đường tròn (C).
Vậy 
Dấu “=” xảy ra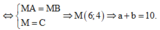 
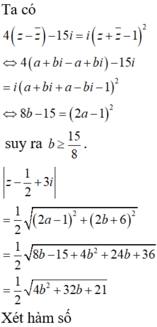
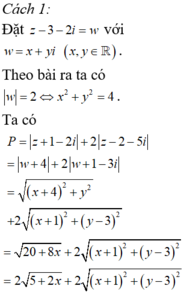
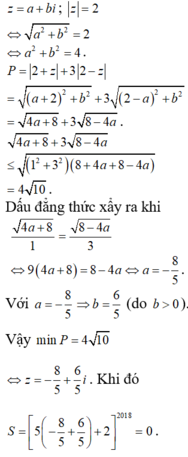
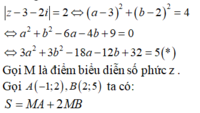
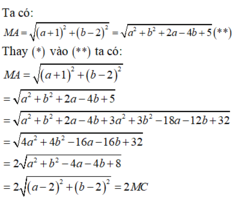
Do \(\left|z\right|=1\Rightarrow z=cosx+i.sinx\) với \(\left\{{}\begin{matrix}a=cosx\\b=sinx\end{matrix}\right.\)
\(z^3-z+2=cos3x+i.sin3x-cosx-i.sinx+2\)
\(=cos3x-cosx+2+i\left(sin3x-sinx\right)\)
\(=-2sin2x.sinx+2+i\left(2cos2x.sinx\right)\)
\(=2\left(-sin2x.sinx+1+i.cos2x.sinx\right)\)
\(\Rightarrow A=\left|z^3-z+2\right|=2\sqrt{\left(1-sin2x.sinx\right)^2+cos^22x.sin^2x}\)
\(=2\sqrt{1+sin^22x.sin^2x-2sin2x.sinx+cos^22x.sin^2x}\)
\(=2\sqrt{1+sin^2x-4sin^2x.cosx}=2\sqrt{2-cos^2x-4cosx\left(1-cos^2x\right)}\)
\(=2\sqrt{2-cos^2x-4cosx+4cos^3x}=2\sqrt{4a^3-a^2-4a+2}\)
\(A_{min}\) khi \(f\left(a\right)=4a^3-a^2-4a+2\) đạt min
\(f'\left(a\right)=12a^2-2a-4=0\Rightarrow\left[{}\begin{matrix}a=-\frac{1}{2}\\a=\frac{2}{3}\end{matrix}\right.\)
Dựa vào BBT, ta thấy \(f\left(a\right)\) min khi \(a=\frac{2}{3}\) \(\Rightarrow b^2=1-a^2=\frac{5}{9}\)
\(\Rightarrow P=\frac{32}{9}\)