Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C.
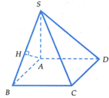

Gọi H là hình chiếu vuông góc của A trên SB.

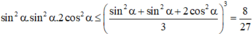
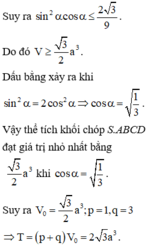

Đáp án C
Phương pháp: Thể tích khối chóp V = 1 3 S d . h : h là chiều cao của khối chóp, S là diện tích đáy.
Phương pháp xác định góc giữa đường thẳng và mặt phẳng: Góc giữa đường thẳng và mặt phẳng chính là góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng.
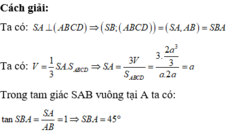
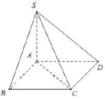

Đáp án C.
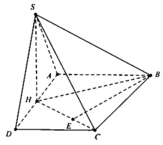
Ta có SAD là tam giác đều nên S H ⊥ A D
Mặt khác S A D ⊥ A B C D ⇒ S H ⊥ A B C D .
Dựng B E ⊥ H C ,
do B E ⊥ S H ⇒ B E ⊥ S H C
Do đó d = B E = 2 a 6 ; S H = a 3 ; A D = 2 a
Do S C = a 15 ⇒ H C = S C 2 − S H 2 = 2 a 3 .
Do S A H B + S C H D = 1 2 a A B + C D = S A B C D 2
suy ra V S . A B C D = 2 V S . H B C = 2 3 . S H . S B C H
= 3 2 a 3 . B E . C H 2 = 4 a 3 6 .
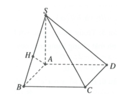

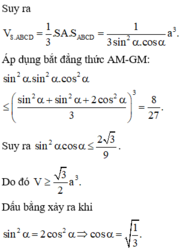
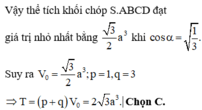

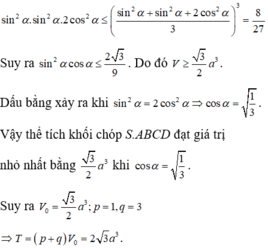

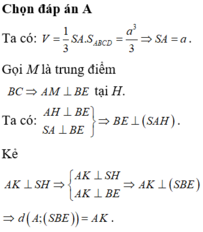

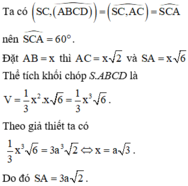

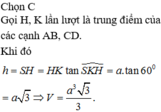
Đáp án C.
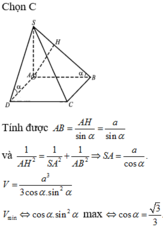
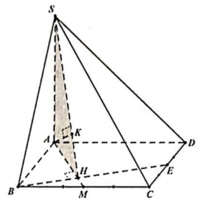
Ta có B C ⊥ A B ; B C ⊥ S A nên B C ⊥ S A B .
Gọi H là hình chiếu vuông góc của A trên SB.
Khi đó A H ⊥ S B C và d A , S B C = A H .
Ta có góc giữa đường thẳng SB và mặt phẳng A B C D là góc S B A ^ .
Đặt S B A ^ = α .
Theo giả thiết ta có A B = a sin α ; S A = a cos α .
Thể tích khối chóp S.ABCD là V = 1 3 . S A . S A B C D = 1 3 sin 2 α cos α a 3 .
Áp dụng bất đẳng thức Cô-si, ta có
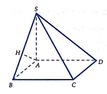
sin 2 α . sin 2 α .2 cos 2 α ≤ sin 2 α + sin 2 α + 2 cos 2 α 3 3 = 8 27
Suy ra sin 2 α cos α ≤ 2 3 9 . Do đó V ≥ 3 2 a 3 .
Dấu bằng xảy ra khi sin 2 α = 2 cos 2 α ⇒ cos α = 1 3 .
Vậy thể tích khối chóp S.ABCD đạt giá trị nhỏ nhất bằng 3 2 a 3 khi cos α = 1 3 .
Suy ra V 0 = 3 2 a 3 ; p = 1, q = 3
⇒ T = p + q V 0 = 2 3 a 3 .