K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 5 2023
2:
a: =>-2x=10
=>x=-5
b: =>(x-3)(2x+5)=0
=>x=3 hoặc x=-5/2
28 tháng 10 2021
1. \(\Leftrightarrow2x^2-3x-2x^2=12\\ \Leftrightarrow-3x=12\\ \Leftrightarrow x=-4\)
2. \(\Leftrightarrow\left(2x-4\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
28 tháng 10 2021
1) \(\Rightarrow2x^2-3x-2x^2=12\Rightarrow-3x=12\Rightarrow x=-4\)
2) \(\Rightarrow2\left(x-3\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
D
2
16 tháng 2 2022
\(\dfrac{x+1}{124}+1+\dfrac{x+2}{123}+1=\dfrac{x+3}{122}+1+\dfrac{x+4}{121}+1\)
\(\Leftrightarrow\dfrac{x+125}{124}+\dfrac{x+125}{123}=\dfrac{x+125}{122}+\dfrac{x+125}{121}\)
\(\Leftrightarrow\left(x+125\right)\left(\dfrac{1}{124}+\dfrac{1}{123}-\dfrac{1}{122}-\dfrac{1}{121}\ne0\right)=0\Leftrightarrow x=-125\)
TD
16 tháng 2 2022
<=>\(\dfrac{x+1}{124}+\dfrac{x+2}{123}-\dfrac{x+3}{122}-\dfrac{x+4}{121}=0\)
<=>\(\left(\dfrac{x+1}{124}+1\right)+\left(\dfrac{x+2}{123}+1\right)-\left(\dfrac{x+3}{122}+1\right)-\left(\dfrac{x+4}{121}+1\right)=0\)
<=>\(\dfrac{x+125}{124}+\dfrac{x+125}{123}-\dfrac{x+125}{122}-\dfrac{x+125}{121}=0\)
<=>\(\left(x+125\right)\left(\dfrac{1}{124}+\dfrac{1}{123}-\dfrac{1}{122}-\dfrac{1}{121}\right)=0\)
<=>x+125=0
<=>x=-125
CM
27 tháng 9 2019
Ta có:
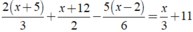
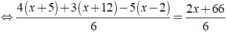
⇔ 4x + 20 + 3x + 36 - 5x + 10 = 2x + 66
⇔ 0x = 0
⇒ Phương trình đã cho vô số nghiệm.
Vậy phương trình đã cho vô số nghiệm.
CM
6 tháng 1 2018
Chọn D
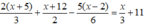
⇔ 4(x + 5) + 3(x + 12) - 5(x – 2) = 2x + 66
⇔ 4x + 20 + 3x + 36 – 5x + 10 = 2x + 66
⇔ 0x = 0 (thỏa mãn mọi giá trị của x)
Vậy phương trình đã cho có vô số nghiệm.
20 tháng 12 2020
1, \(45+x^3-5x^2-9x=9\left(5-x\right)+x^2\left(x-5\right)\)
\(=\left(9-x^2\right)\left(x-5\right)=\left(3-x\right)\left(x+3\right)\left(x-5\right)\)
3, \(x^4-5x^2+4\)
Đặt \(x^2=t\left(t\ge0\right)\)ta có :
\(t^2-5t+4=t^2-t-4t+4=t\left(t-1\right)-4\left(t-1\right)\)
\(=\left(t-4\right)\left(t-1\right)=\left(x^2-4\right)\left(x^2-1\right)=\left(x-2\right)\left(x+2\right)\left(x-1\right)\left(x+1\right)\)
YN
29 tháng 3 2022
`Answer:`
1. `45+x^3-5x^2-9x`
`=x^3+3x^2-8x^2-24x+15x+45x`
`=x^2 .(x+3)-8x.(x+3)+15.(x+3)`
`=(x+3).(x^2-8x+15)`
`=(x+3).(x^2-5x-3x+15)`
`=(x-3).(x-5).(x-3)`
2. `x^4-2x^3-2x^2-2x-3`
`=x^4+x^3-3x^3+x^2+x-3x-3`
`=x^3 .(x+1)-3x^2 .(x+1)+x.(x+1)-3.(x+1)`
`=(x+1).(x^3-3x^2+x-3)`
`=(x+1).[x^3 .(x-3).(x-3)]`
`=(x+1).(x-3).(x^2+1)`
3. `x^4-5x^2+4`
`=x^4-x^2-4x^2+4`
`=x^2 .(x^2-1)-4.(x^2-1)`
`=(x^2-1).(x^2-4)`
`=(x-1).(x+1).(x-2).(x+2)`
4. `x^4+64`
`=x^4+16x^2+64-16x^2`
`=(x^2+8)^2-16x^2`
`=(x^2+8-4x).(x^2+8+4x)`
5. `x^5+x^4+1`
`=x^5+x^4+x^3-x^3+1`
`=x^3 .(x^2+x+1)-(x^3-1)`
`=x^3 .(x^2+x+1)-(x-1).(x^2+x+1)`
`=(x^2+x+1).(x^3-x+1)`
6. `(x^2+2x).(x^2+2x+4)+3`
`=(x^2+2x)^2+4.(x^2+2x)+3`
`=(x^2+2x)^2+x^2+2x+3.(x^2+2x)+3`
`=(x^2+2x+1).(x^2+2x)+3.(x^2+2x+1)`
`=(x^2+2x+1).(x^2+2x+3)`
`=(x+1)^2 .(x^2+2x+3)`
7. `(x^3+4x+8)^2+3x.(x^2+4x+8)+2x^2`
`=x^6+8x^4+16x^3+16x^2+64x+64+3x^3+12x^2+24x+2x^2`
`=x^6+8x^4+19x^3+30x^2+88x+64`
8. `x^3 .(x^2-7)^2-36x`
`=x[x^2.(x^2-7)^2-36]`
`=x[(x^3-7x)^2-6^2]`
`=x.(x^3-7x-6).(x^3-7x+6)`
`=x.(x^3-6x-x-6).(x^3-x-6x+6)`
`=x.[x.(x^2-1)-6.(x+1)].[x.(x^2-1)-6.(x-1)]`
`=x.(x+1).[x.(x-1)-6].(x-1).[x.(x+1)-6]`
`=x.(x+1).(x-1).(x^2-3x+2x-6).(x^2+3x-2x-6)`
`=x.(x+1).(x-1).[x.(x-3)+2.(x-3)].[x.(x+3)-2.(x+3)]`
`=x.(x+1)(x-1).(x-2).(x+2).(x-3).(x+3)`
9. `x^5+x+1`
`=x^5-x^2+x^2+x+1`
`=x^2 .(x^3-1)+(x^2+x+1)`
`=x^2 .(x-1).(x^2+x+1)+(x^2+x+1)`
`=(x^2+x+1).(x^3-x^2+1)`
10. `x^8+x^4+1`
`=[(x^4)^2+2x^4+1]-x^4`
`=(x^4+1)^2-(x^2)^2`
`=(x^4-x^2+1).(x^4+x^2+1)`
`=[(x^4+2x^2+1)-x^2].(x^4-x^2+1)`
`=[(x^2+1)^2-x^2].(x^4-x^2+1)`
`=(x^2-x+1).(x^2+x+1).(x^4-x^2+1)
11. ` x^5-x^4-x^3-x^2-x-2`
`=x^5-2x^4+x^4-2x^3+x^3-2x^2+x^2-2x+x-2`
`=x^4 .(x-2)+x^3 ,(x-2)+x^2 .(x-2)+x.(x-2)+(x-2)`
`=(x-2).(x^4+x^3+x^2+x+1)`
12. `x^9-x^7-x^6-x^5+x^4+x^3+x^2-1`
`=(x^9-x^7)-(x^6-x^4)-(x^5-x^3)+(x^2-1)`
`=x^7 .(x^2-1)-x^4 .(x^2-1)-x^3 .(x^2-1)+(x^2-1)`
`=(x^2-1).(x^7-x^4-x^3+1)`
`=(x-1)(x+1)(x^3-1)(x^4-1)`
`=(x-1)(x+1)(x^2+x+1)(x-1)(x^2-1)(x^2+1)`
`=(x-1)^2 .(x+1)(x^2+x+1)(x-1)(x+1)(x^2+1)`
`=(x-1)^3 .(x+1)^2 .(x^2+x+1)(x^2+1)`
13. `(x^2-x)^2-12(x^2-x)+24`
`=[ (x^2-x)^2-2.6(x^2-x)+6^2]-12`
`=(x^2-x+6)^2-12`
`=(x^2-x+6-\sqrt{12})(x^2-x+6+\sqrt{12})`
22 tháng 9 2020
a) ( x + 2 )( x + 3 ) - ( x - 2 )( x + 5 )
= x2 + 5x + 6 - ( x2 + 3x - 10 )
= x2 + 5x + 6 - x2 - 3x + 10
= 2x + 16
b) ( 8 - 5x )( x + 2 ) + 4( x - 2 )( x + 1 ) + 2( x - 2 )( x + 2 ) + 10
= -5x2 - 2x + 16 + 4( x2 - x - 2 ) + 2( x2 - 4 ) + 10
= -5x2 - 2x + 16 + 4x2 - 4x - 8 + 2x2 - 8 + 10
= x2 - 6x + 10
c) 4( x - 1 )( x + 5 ) - ( x + 2 )( x + 5 ) - 3( x - 1 )( x + 2 )
= 4( x2 + 4x - 5 ) - ( x2 + 7x + 10 ) - 3( x2 + x - 2 )
= 4x2 + 16x - 20 - x2 - 7x - 10 - 3x2 - 3x + 6
= 6x - 24
d) ( x - 1 )( x5 + x4 + x3 + x2 + x + 1 )
= x6 + x5 + x4 + x3 + x2 + x - x5 - x4 - x3 - x2 - x - 1
= x6 - 1
\(\left(x-1\right)\left(x-2\right)\left(x+4\right)\left(x+5\right)=122\)
\(\Leftrightarrow\left(x^2+3x-4\right)\left(x^2+3x-10\right)=122\)
Đặt \(x^2+3x-4=t\)
\(\Leftrightarrow t\left(t-6\right)=122\Leftrightarrow t^2-6t-122=0\Leftrightarrow t=3\pm\sqrt{131}\)
đề có lỗi ko bạn ?