Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
Giả sử chiếc đu quay quay theo chiều kim đồng hồ.
Gọi M là vị trí của cabin, M’ là vị trí của cabin sau 20 phút và các điểm A A’, B, H như hình dưới.
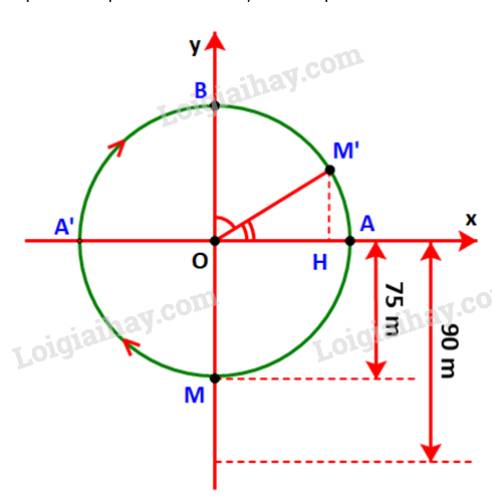
Vì đi cả vòng quay mất 30 phút nên sau 20 phút, cabin sẽ đi quãng đường bằng \(\frac{2}{3}\) chu vi đường tròn.
Sau 15 phút cabin đi chuyển từ điểm M đến điểm B, đi được \(\frac{1}{2}\) chu vi đường tròn.
Trong 5 phút tiếp theo cabin đi chuyển từ điểm B đến điểm M’ tương ứng \(\frac{1}{6}\) chu vi đường tròn hay \(\frac{1}{3}\) cung .
Do đó: \(\widehat {BOM'} = \frac{1}{3}{.180^o} = {60^o}\)\( \Rightarrow \widehat {AOM'} = {90^o} - {60^o} = {30^o}.\)
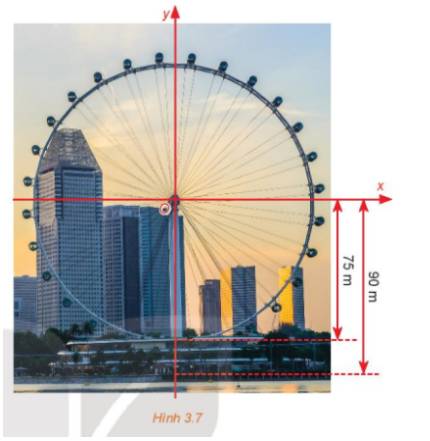
\( \Rightarrow M'H = \sin {30^o}.OM' = \frac{1}{2}.75 = 37,5\left( m \right).\)
\( \Rightarrow \) Độ cao của người đó là: 37,5 + 90 = 127,5 (m).
Vậy sau 20 phút quay người đó ở độ cao 127,5 m.

Đặt AB=a
=>\(MB=MN=a\sqrt{10};BN=2a\sqrt{5}\)
=>ΔBMN vuông cân tại M và J là trung điểm của BN
=>MJ vuông góc NJ
=>NJ: x-5=0
Tọa độ J là:
x-5=0 và 2y-7=0
=>x=5 và y=7/2
Vì J là trung điểm của BN nên B(5;1)
Gọi C(x,y), x>3
BC=2NC=2 căn 5
Ta có HPT:
(x-5)^2+(y-1)^2=20 và (x-5)^2+(y-6)^2=5
=>x=7 và y=5(nhận) hoặc x=3 và y=5(loại)
=>C(7;5)

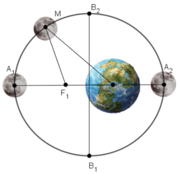
Theo đề bài có:
Độ dài trục lớn của elip bằng 769266km ⇒ A1A2 = 2a = 769266 ⇒ a = 384633
Độ dài trục nhỏ của elip bằng 768106km ⇒ B1B2 = 2b = 768106 ⇒ b = 384053
⇒ c2 = a2 – b2 = 445837880 ⇒ c ≈ 21115
⇒ F1F2 = 2c = 42230
⇒ A1F1 = A2F2 = (A1A2 – F1F2)/2 = 363518
+ Trái Đất gần Mặt Trăng nhất khi Mặt Trăng ở điểm A2
⇒ khoảng cách ngắn nhất giữa Trái Đất và Mặt Trăng bằng A2F2 = 363518 km
+ Trái Đất xa Mặt Trăng nhất khi Mặt Trăng ở điểm A1
⇒ khoảng cách xa nhất giữa Trái Đất và Mặt Trăng bằng:
A1F2 = A1F1 + F1F2 = 405748 km.

Tam giác ABC vuông tại B nên ta có: \(\tan C = \frac{{AB}}{{CB}} \Leftrightarrow AB = \tan {32^ \circ }.(1 + x)\)
Tam giác ADB vuông tại B nên ta có: \(\tan D = \frac{{AB}}{{DB}} \Leftrightarrow AB = \tan {40^ \circ }.x\)
\(\begin{array}{l} \Rightarrow \tan {32^ \circ }.(1 + x) = \tan {40^ \circ }.x\\ \Leftrightarrow x.(\tan {40^ \circ } - \tan {32^ \circ }) = \tan {32^ \circ }\\ \Leftrightarrow x = \frac{{\tan {{32}^ \circ }}}{{\tan {{40}^ \circ } - \tan {{32}^ \circ }}}\\ \Leftrightarrow x \approx 2,9\;(km)\end{array}\)
\( \Rightarrow AB \approx \tan {40^ \circ }.2,92 \approx 2,45\;(km)\)
Vậy chiều cao của ngọn núi là 2,45 km.

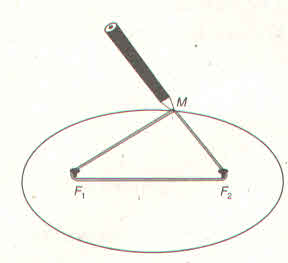
Ta có: 2a = 80 => a = 40
2b = 40 => b = 20
c2 = a2 – b2 = 1200 => c = 20√3
Phải đóng đinh tại các điểm F1 , F2 và cách mép ván:
F2A = OA – OF2 = 40 - 20√3
=> F2A = 20(2 - √3) ≈ 5,4cm
Chu vi vòng dây bằng: F1.F2+ 2a = 40√3 + 80
=> F1.F2 + 2a = 40(2 + √3)
F1.F2 + 2a ≈ 149,3cm

_ Khi gặp nhau lần thứ nhất thì hai bố con đã chạy được \(\frac{1}{2}\) vòng đua .
_ Khi gặp lần 2 thì 2 bố con đã chạy thêm được 1 vòng nữa .
_ Tổng số hai bố con đã chạy được : 1,5 vòng .
_Chỗ hai bố con gặp nhau con đã chạy quá nửa vòng là 60 mét .
Nửa chu vi đường chạy là :
100 x ( 1,5 : 0,5 ) - 60 = 240 ( m )
Chu vi vòng chạy là :
240 x 2 = 480 ( m )
Đáp số : 480 m .
Gọi nửa vòng tròn sân vận động là S, ta có lần gặp nhau đâu tiền hai bố con đã đi được quãng đường là S. Kể từ lần gặp đầu đến lần gặp thứ hai, cả hai bố con đi thêm được chu vi của đường tròn (tức là 2xS). Vậy lần gặp nhau thứ hai thì hai bố con đã đi được quãng đường là 3xS và thời gian gặp lần sau gấp 3 lần thời gian gặp lần đầu, Vậy suy ra lần gặp nhau thứ hai người con đã đi được quãng đường gấp 3 lần quãng đường lần gặp thứ nhất.
Vậy quãng đường người con đã đi lần gặp thứ hai là:
S + 60 = 100 x 3
S + 60 = 300 (m)
S = 300 - 60
S = 240 (m)
Vậy chu vi vòng tròn là:
S x 2 = 240 x 2
S x 2 = 480 (m)
Đáp số: 480m
tick nha Phạm Thị Mỹ Tình 
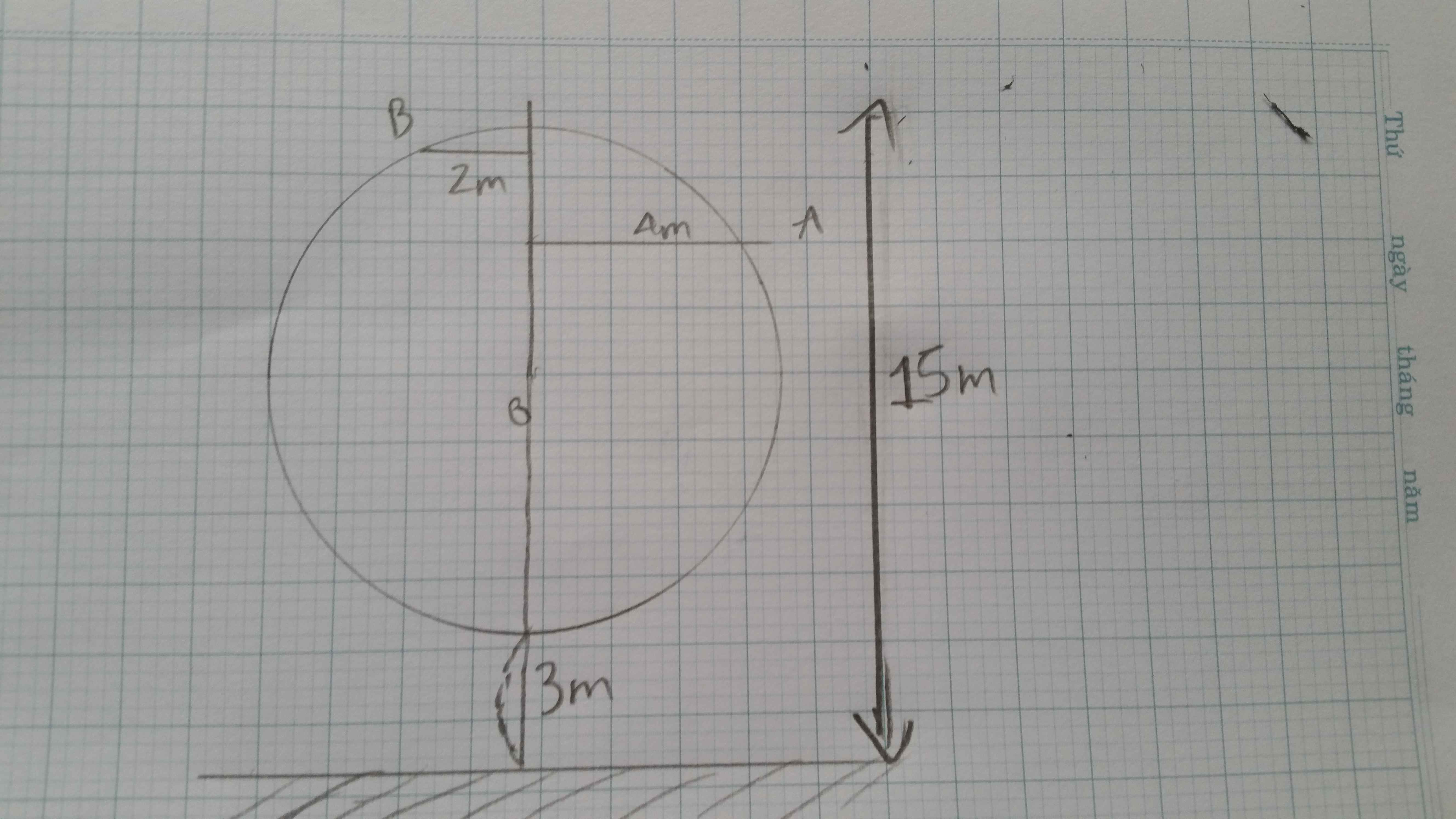



Gọi hình chiếu của B trên trục là H. Tâm đu quay là O.
Dễ thấy đường kính đu quay là 15 - 3 = 12 (m) nên OB = R = 6m.
Theo định lý Pytago ta có \(OH=\sqrt{OB^2-BH^2}=\sqrt{6^2-2^2}=4\sqrt{2}\) (m).
Gọi hình chiếu của B trên mặt đất là K, N là hình chiếu của O trên mặt đất. Ta có \(BK=HN=HO+ON=4\sqrt{2}+6+3=9+4\sqrt{2}\) (m)
Tương tự ta tính được khoảng cách từ C xuống mặt đất
Vậy....