Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng giả thiết và một đánh giá quen thuộc, ta được: \(16\left(a+b+c\right)\ge\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{ab+bc+ca}{abc}=\frac{\left(ab+bc+ca\right)^2}{abc\left(ab+bc+ca\right)}\ge\frac{3\left(a+b+c\right)}{ab+bc+ca}\)hay \(\frac{1}{6\left(ab+bc+ca\right)}\le\frac{8}{9}\)
Đến đây, ta cần chứng minh \(\frac{1}{\left(a+b+\sqrt{2\left(a+c\right)}\right)^3}+\frac{1}{\left(b+c+\sqrt{2\left(b+a\right)}\right)^3}+\frac{1}{\left(c+a+\sqrt{2\left(c+b\right)}\right)^3}\le\frac{1}{6\left(ab+bc+ca\right)}\)
Áp dụng bất đẳng thức Cauchy cho ba số dương ta có \(a+b+\sqrt{2\left(a+c\right)}=a+b+\sqrt{\frac{a+c}{2}}+\sqrt{\frac{a+c}{2}}\ge3\sqrt[3]{\frac{\left(a+b\right)\left(a+c\right)}{2}}\)hay \(\left(a+b+\sqrt{2\left(a+c\right)}\right)^3\ge\frac{27\left(a+b\right)\left(a+c\right)}{2}\Leftrightarrow\frac{1}{\left(a+b+2\sqrt{a+c}\right)^3}\le\frac{2}{27\left(a+b\right)\left(a+c\right)}\)
Hoàn toàn tương tự ta có \(\frac{1}{\left(b+c+2\sqrt{b+a}\right)^3}\le\frac{2}{27\left(b+c\right)\left(b+a\right)}\); \(\frac{1}{\left(c+a+2\sqrt{c+b}\right)^3}\le\frac{2}{27\left(c+a\right)\left(c+b\right)}\)
Cộng theo vế các bất đẳng thức trên ta được \(\frac{1}{\left(a+b+\sqrt{2\left(a+c\right)}\right)^3}+\frac{1}{\left(b+c+\sqrt{2\left(b+a\right)}\right)^3}+\frac{1}{\left(c+a+\sqrt{2\left(c+b\right)}\right)^3}\le\frac{4\left(a+b+c\right)}{27\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được \(\frac{4\left(a+b+c\right)}{27\left(a+b\right)\left(b+c\right)\left(c+a\right)}\le\frac{1}{6\left(ab+bc+ca\right)}\)\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge\frac{8}{9}\left(ab+bc+ca\right)\left(a+b+c\right)\)
Đây là một đánh giá đúng, thật vậy: đặt a + b + c = p; ab + bc + ca = q; abc = r thì bất đẳng thức trên trở thành \(pq-r\ge\frac{8}{9}pq\Leftrightarrow\frac{1}{9}pq\ge r\)*đúng vì \(a+b+c\ge3\sqrt[3]{abc}\); \(ab+bc+ca\ge3\sqrt[3]{\left(abc\right)^2}\))
Vậy bất đẳng thức được chứng minh
Đẳng thức xảy ra khi \(a=b=c=\frac{1}{4}\)

ko cả biết BĐT AM-GM với C-S là gì còn hỏi bài này rảnh háng
Đề sai rồi. Nếu như là a, b, c dương thì giá trị nhỏ nhất của nó phải là 9 mới đúng. Còn để có GTNN như trên thì điều kiện là a, b, c không âm nhé. Mà bỏ đi e thi cái gì mà phải giải câu cỡ này. Cậu này mạnh lắm đấy không phải dạng thường đâu.

Đặt \(\left(\frac{1}{a},\frac{1}{b},\frac{1}{c}\right)=\left(x,y,z\right)\)
\(x+y+z\ge\frac{x^2+2xy}{2x+y}+\frac{y^2+2yz}{2y+z}+\frac{z^2+2zx}{2z+x}\)
\(\Leftrightarrow x+y+z\ge\frac{3xy}{2x+y}+\frac{3yz}{2y+z}+\frac{3zx}{2z+x}\)
\(\frac{3xy}{2x+y}\le\frac{3}{9}xy\left(\frac{1}{x}+\frac{1}{x}+\frac{1}{y}\right)=\frac{1}{3}\left(x+2y\right)\)
\(\Rightarrow\Sigma_{cyc}\frac{3xy}{2x+y}\le\frac{1}{3}\left[\left(x+2y\right)+\left(y+2z\right)+\left(z+2x\right)\right]=x+y+z\)
Dấu "=" xảy ra khi x=y=z

\(\Leftrightarrow\Sigma\sqrt{\frac{3a^3}{\left[5a^2+\left(b+c\right)^2\right]\left(a+b+c\right)}}\le1\)
Theo Am-GM: \(VT=\Sigma\sqrt{\frac{3a^2}{5a^2+\left(b+c\right)^2}.\frac{a}{a+b+c}}\le\Sigma\frac{3a^2}{2\left(5a^2+\left(b+c\right)^2\right)}+\frac{1}{2}\)
Như vậy nó là đủ để chứng minh rằng: \(\Sigma\frac{3a^2}{5a^2+\left(b+c\right)^2}\le1\)
Giả sử \(c=min\left\{a,b,c\right\}\) nó tương đương:
![]()
(Gõ Latex, không hiện thì vô thống kê hỏi đáp xem)
Đây là điều hiển nhiên/
PS: Bài này quan trọng là ý tưởng phá căn thôi chứ không có gì khó. Lúc đầu UCT bất đẳng thức cuối cho đẹp nhưng phải xét các TH mệt lắm, chưa rành nên không làm cách đó:D
Chứng minh: \(\Sigma\frac{3a^2}{5a^2+\left(b+c\right)^2}\le1\), cách 2:
Đổi biến sang pqr: (Vô thống kê hỏi đáp xem nếu olm không hiện Latex)
Nếu \(p^2\le4q\) ta cần:
![]()
(Hiển nhiên)
Nếu \(p^2\ge4q\) thì cần chứng minh:
![]()
(Hiển nhiên)
Từ 2 TH trên ta thu được điều phải chứng minh.

a )
Áp dụng BĐT Bunhiacopxki ta có :
\(\left(b^2+\left(c+a\right)^2\right)\left(1+\right)\ge\left(b+2\left(a+c\right)\right)^2\)
\(\Rightarrow\sqrt{\frac{a^2}{b^2+\left(c+a\right)^2}}\le\sqrt{5}.\frac{a}{b+2c+2a}\)
\(\Rightarrow VT\le\sqrt{5}.\left(\frac{a}{b+2c+2a}+\frac{b}{c+2a+2b}+\frac{c}{a+2b+2c}\right)\)
Cần chứng minh : \(\frac{a}{b+2c+2a}+\frac{b}{c+2a+2b}+\frac{c}{a+2b+2c}\le\frac{3}{5}\)
\(\Leftrightarrow\left(\frac{1}{2}-\frac{a}{b+2c+2a}\right)+\left(\frac{1}{2}-\frac{b}{c+2a+2b}\right)+\left(\frac{1}{2}-\frac{c}{a+2b+2c}\right)\ge\frac{9}{10}\)
\(\Leftrightarrow\frac{b+2c}{b+2c+2a}+\frac{c+2a}{c+2a+2b}+\frac{a+2b}{a+2b+2c}\ge\frac{9}{5}\)
Áp dụng BĐT Bunhiacopxki dạng phân thức ở vế trái :
\(\Rightarrow VT\ge\frac{\left(b+2c+c+2a+a+2b\right)^2}{\left(b+2c\right)^2+2a\left(b+2c\right)+\left(c+2a\right)^2+2b\left(c+2a\right)+\left(a+2b\right)^2+2c\left(a+2b\right)}\)
\(=\frac{9\left(a+b+c\right)^2}{5\left(a+b+b\right)^2}=\frac{9}{5}\left(đpcm\right)\)
Dấu " = '" xảy ra khi a=b=c
b ) Ta có abc =1
Ta chứng minh :
\(\frac{1}{ab+a+1}+\frac{1}{bc+b+1}+\frac{1}{ac+c+1}=1\)
VT \(=\frac{1}{ab+a+1}+\frac{a}{abc+ab+a}+\frac{ab}{a^2bc+abc+ac}\)
\(=\frac{1}{ab+a+1}+\frac{a}{ab+a+1}+\frac{ab}{ab+a+1}=1\left(đpcm\right)\)
Ta có : \(\left(1+a\right)^2+b^2+5=\left(a^2+b^2\right)+2a+6\ge2ab+2a+6\)
\(\Rightarrow\frac{\left(1+a\right)^2+b^2+5}{ab+a+4}=\frac{2ab+2a+6}{ab+a+4}=2-\frac{2}{ab+a+4}\)
Mà \(\frac{1}{ab+a+4}=\frac{1}{ab+a+1+3}\le\frac{1}{4}\left(\frac{1}{ab+a+1}+\frac{1}{3}\right)\) ( do \(\frac{1}{x+y}\le\frac{1}{4}\left(\frac{1}{x}+\frac{1}{y}\right)\)
\(\Rightarrow\frac{\left(1+a\right)^2+b^2+5}{ab+a+4}\ge2-\frac{1}{2}\left(\frac{1}{ab+a+1}+\frac{1}{3}\right)=\frac{11}{6}-\frac{1}{2}.\frac{1}{ab+a+1}\)
Khi đó :
\(P\ge\frac{11}{2}-\frac{1}{2}.\left(\frac{1}{ab+a+1}+\frac{1}{bc+b+1}+\frac{1}{ac+c+1}\right)=\frac{11}{2}-\frac{1}{2}.1=5\)
\(P_{Min}=5\) khi \(a=b=c=1\)

\(=\)\(18\left(\frac{1}{1}+\frac{1}{1}+\frac{1}{1}\right)\)\(=\)\(18\frac{3}{1}\)\(>\)\(\left(9+5\sqrt{3}\right)\left(a^2+b^2+c^2\right)\)\(=\)\(0\)
Vậy\(18\frac{3}{1}\)\(>\)\(0\)
Chứng minh là \(18\frac{3}{1}\)\(>\)\(0\)là đúng
chúc bạn học tốt
Bất đẳng thức trên
<=> 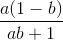 + 1 +
+ 1 + 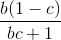 + 1 +
+ 1 + 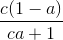 + 1 ≥ 3
+ 1 ≥ 3
<=> 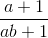 +
+ 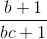 +
+ 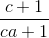 ≥ 3 (*)
≥ 3 (*)
Ta có: VT(*) ≥ 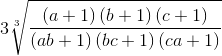
Ta sẽ chứng minh: (a + 1)(b + 1)(c + 1) ≥ (ab + 1)(bc + 1)(ca + 1)
<=> abc + ab + bc + ca + a + b + c + 1
≥ a2b2c2 + abc(a + b + c) + ab + bc + ca + 1
<=> 3 ≥ a2b2c2 + 2abc (**)
Theo Cosi: 3 = a + b + c ≥ 3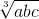 =>
=> 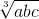 ≤ 1 => abc ≤ 1
≤ 1 => abc ≤ 1
Vậy (**) đúng => (*) đúng.
t chuyên Anh mà:v
tth_newrì lí.-. thế lm Toán giỏi phết.Toàn cho mấy bài toán hack não không.Để tìm lại cái não đã bị hack r