Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Vì OA, OB, OC đôi một vuông góc và M là trực tâm tam giác ABC => OM ⊥ (ABC)
Suy ra mp(ABC) nhận O M → làm véc tơ pháp tuyến và đi qua điểm M(1;2;3)
Vậy phương trình mp(P):
![]()
<=> x +2y+3z -14=0

Chọn B
Gọi B (0;0;b) là giao điểm của đường thẳng d và trục Oz.
![]()
Vì đường thẳng d song song với mặt phẳng (P) nên:
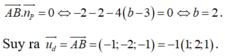

Đáp án D.
Gọi A, B, C lần lượt là hình chiếu của M trên các trục Ox, Oy, Oz.
Suy ra A(1;0;0), B(0;2;0), C(0;0;3)
Phương trình:
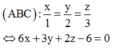

Đáp án D
Phương pháp: Giả sử đường thẳng (d) cắt trục Oz tại điểm B(0;0;b)
![]()
Cách giải:
Giả sử đường thẳng (d) cắt trục Oz tại điểm B(0;0;b)
![]()
![]()
![]()
![]()



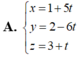
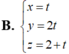
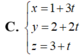
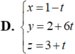

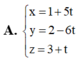
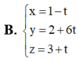




Giả sử mặt phẳng (P) cần tìm có phương trình dạng :
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)
với \(abc\ne0\) thỏa mãn
\(\frac{1}{a}+\frac{2}{b}+\frac{3}{c}=1\) (1)
Do (P) đi qua M và \(\left|a\right|=\left|b\right|=\left|c\right|\) (2)
(Do (P) chắn trên 3 trục tọa độ các đoạn thẳng có độ dài bằng nhau)
Từ (2) suy ra hoặc \(a=b=c\) hoặc \(a=-b=c\) hoặc \(a=b=-c\) hoặc \(b=c=-a\)
* Nếu \(a=b=c\), thay vào (1) ta được \(\frac{1}{a}+\frac{2}{a}+\frac{3}{a}=1\Leftrightarrow a=6\) do đó phương trình mặt phẳng (P) : \(\frac{x}{6}+\frac{y}{6}+\frac{z}{6}=1\) hay \(x+y+z-6=0\)
* Nếu \(a=-b=c\), thay vào (1) ta được \(\frac{1}{a}-\frac{2}{a}+\frac{3}{a}=1\Leftrightarrow a=2\) do đó phương trình mặt phẳng (P) : \(\frac{x}{2}-\frac{y}{2}+\frac{z}{2}=1\) hay \(x-y+z-2=0\)
* Nếu \(a=b=-c\), thay vào (1) ta được \(\frac{1}{a}+\frac{2}{a}-\frac{3}{a}=1\Leftrightarrow\) Vô nghiệm
* Nếu \(b=c=-a\), thay vào (1) ta được \(\frac{1}{a}-\frac{2}{a}-\frac{3}{a}=1\Leftrightarrow a=-4\) do đó phương trình mặt phẳng (P) : \(\frac{x}{-4}-\frac{y}{4}+\frac{z}{4}=1\) hay \(-x+y+z-4=0\)
Vậy qua điểm \(M\left(1;2;3\right)\) có 3 mặt phẳng tọa độ yêu cầu, đó là:
\(\left(P_1\right):x+y+z-6=0\) chắn trên 3 trục tọa độ các đoạn có độ dài bằng 6
\(\left(P_2\right):x-y+z-2=0\) chắn trên 3 trục tọa độ các đoạn có độ dài bằng 2
\(\left(P_3\right):-x+y+z-4=0\)chắn trên 3 trục tọa độ các đoạn có độ dài bằng 4