Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét đường thẳng bất kỳ đi qua điểm E có dạng
\(\Delta:a\left(x-2\right)+b\left(y+1\right)=0\)
ta có
\(d\left(\text{F},\Delta\right)=\frac{\left|-5a\right|}{\sqrt{a^2+b^2}}=3\Leftrightarrow16a^2-9b^2=0\Leftrightarrow\orbr{\begin{cases}4a=3b\\4a=-3b\end{cases}}\)
vậy có hai đường thẳng thỏa mãn là : \(\orbr{\begin{cases}3\left(x-3\right)+4\left(y+1\right)=0\\3\left(x-3\right)-4\left(y+1\right)=0\end{cases}}\)

\(\overrightarrow{EF}=\left(1;0\right)\Rightarrow EF=1\)
\(\Rightarrow\) Khoảng cách tối đa mà đường thẳng qua E có thể cách F là 1 đoạn bằng 1
\(\Rightarrow\) Không tồn tại đường thẳng thỏa mãn yêu cầu đề bài

\(AC=\sqrt{\left(3-1\right)^2+\left(0+2\right)^2}=2\sqrt{2}< 3\)
\(\Rightarrow\) Không tồn tại đường thẳng denta thỏa mãn yêu cầu đề bài

Gọi \(\Delta \) là đường thẳng đi qua B và có vecto pháp tuyến là \(\overrightarrow n = \left( {a;b} \right)\)
Vậy phương trình \(\Delta \) là: \(a\left( {x + 1} \right) + b\left( {y - 2} \right) = 0 \Leftrightarrow {\rm{a}}x + by + \left( {a - 2b} \right) = 0\)
Ta có: \(d\left( {A,\Delta } \right) = d\left( {C,\Delta } \right) \Leftrightarrow \frac{{\left| {3a + 2b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \frac{{\left| {4a - 3b} \right|}}{{\sqrt {{a^2} + {b^2}} }} \Leftrightarrow \left[ \begin{array}{l}3a + 2b = 4a - 3b\\3a + 2b = - 4a + 3b\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = 5b\left( 1 \right)\\7a = b\left( 2 \right)\end{array} \right.\)
Từ (1) ta có thể chọn được 1 vecto pháp tuyến là: \(\overrightarrow n = \left( {5;1} \right)\). Vậy phương trình đường thẳng \(\Delta \)là: \(5x + y + 3 = 0\)
Từ (2) ta có thể chọn được 1 vecto pháp tuyến là: \(\overrightarrow n = \left( {1;7} \right)\). Vậy phương trình đường thẳng \(\Delta \)là: \(x + 7y - 13 = 0\)
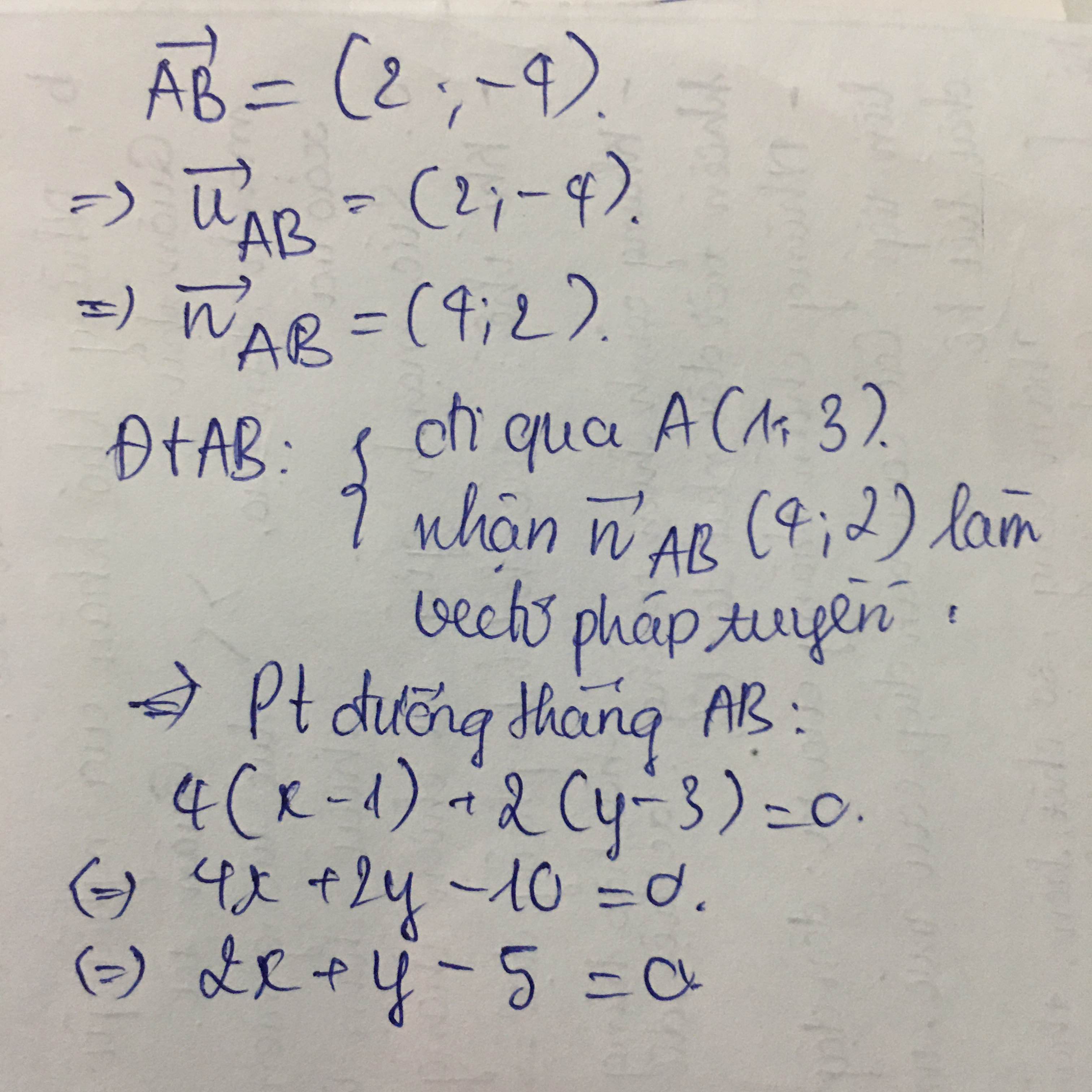
Gọi phương trình đường thẳng d qua E có dạng:
\(a\left(x-2\right)+b\left(y+1\right)=0\Leftrightarrow ax+by-2a+b=0\)
\(d\left(F;d\right)=3\Leftrightarrow\dfrac{\left|-3a-b-2a+b\right|}{\sqrt{a^2+b^2}}=3\)
\(\Leftrightarrow\left|5a\right|=3\sqrt{a^2+b^2}\)
\(\Leftrightarrow25a^2=9a^2+9b^2\)
\(\Leftrightarrow16a^2=9b^2\Rightarrow\left\{{}\begin{matrix}4a=3b\\4a=-3b\end{matrix}\right.\)
Chọn \(\left(a;b\right)=\left(3;4\right);\left(3;-4\right)\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}3x+4y-2=0\\3x-4y-10=0\end{matrix}\right.\)