Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\({\left[ {{{\left( { - \frac{1}{6}} \right)}^3}} \right]^4}\) (với \(a = - \frac{1}{6}\))
\(=(- \frac{1}{6})^{3. 4}=(- \frac{1}{6})^{12}\)
b)\({\left[ {{{\left( { - 0,2} \right)}^4}} \right]^5}\) (với \(a = - 0,2\))
\(=(-0,2)^{4.5}=(-0,2)^{20}\)

\(\begin{array}{l}a){( - 2)^3}.{( - 2)^4} = {( - 2)^{3 + 4}} = {( - 2)^7}\\b){(0,25)^7}:{(0,25)^3} = {(0,25)^{7 - 3}} = {(0,25)^4}\end{array}\)

a) \({\left( {\frac{8}{9}} \right)^3} \cdot \frac{4}{3} \cdot \frac{2}{3} = {\left( {\frac{8}{9}} \right)^3}.\frac{8}{9} = {\left( {\frac{8}{9}} \right)^{3+1}}={\left( {\frac{8}{9}} \right)^4}\)
b) \({\left( {\frac{1}{4}} \right)^7} \cdot 0,25 = {\left( {0,25} \right)^7}.0,25 ={\left( {0,25} \right)^{7+1}}= {\left( {0,25} \right)^8}\)
c) \({( - 0,125)^6}:\frac{{ - 1}}{8} = {\left( {\frac{{ - 1}}{8}} \right)^6}:\frac{{ - 1}}{8} = {\left( {\frac{{ - 1}}{8}} \right)^{6-1}}= {\left( {\frac{{ - 1}}{8}} \right)^5}\)
d) \({\left[ {{{\left( {\frac{{ - 3}}{2}} \right)}^3}} \right]^2} = {\left( {\frac{{ - 3}}{2}} \right)^{3.2}} = {\left( {\frac{{ - 3}}{2}} \right)^6}\)

Bài 6:
a: \(2^{27}=8^9\)
\(3^{18}=9^9\)
b: Vì \(8^9< 9^9\)
nên \(2^{27}< 3^{18}\)

a) \(\dfrac{2^{14}.3^{12}}{6^{11}}\)
\(=\dfrac{2^2.2^{12}.3^{12}}{6^{11}}\)
\(=\dfrac{4.6^{12}}{6^{11}}\)
\(=4.6\)
\(=24\)

\(27^3:9\left[\left(-3\right)^2\right]^2=3^9:3^2\cdot3^4=3^{9-2+4}=3^{11}\)

a) \(\frac{6}{5}.{\left( {1,2} \right)^8} = 1,2.{(1,2)^8} = {(1,2)^{1 + 8}} = {(1,2)^9}\)
b) \({\left( {\frac{{ - 4}}{9}} \right)^7}:\frac{{16}}{{81}} = {\left( {\frac{{ - 4}}{9}} \right)^7}:{\left( {\frac{{ - 4}}{9}} \right)^2} = {\left( {\frac{{ - 4}}{9}} \right)^{7 - 2}} = {\left( {\frac{{ - 4}}{9}} \right)^5}\)
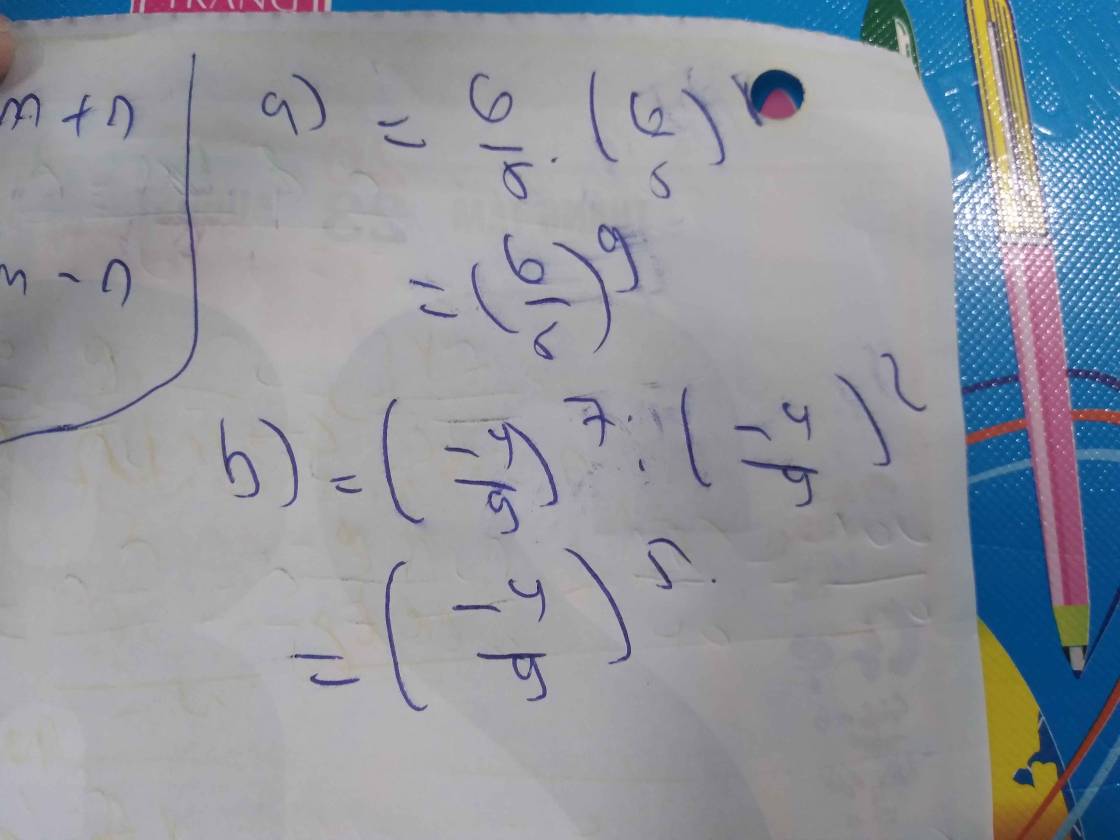
a) \({2^m}{.2^n}=\underbrace {2.2 \ldots .2}_{m{\rm{ }}}{\rm{ }}.\underbrace {2.2 \ldots .2}_{n{\rm{ }}}{\rm{ }}\) = 2m+n
b) \({3^m}:{3^n}=(\underbrace {3.3 \ldots .3}_{m{\rm{ }}}{\rm{ }}):(\underbrace {3.3 \ldots .3}_{n{\rm{ }}}{\rm{ }})\) = 3m-n với \(m \ge n\)