Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn nhập lại hai hàm số đó nhé chính giữa mik không biết là dấu + hay -

a) Đồ thị hàm số y = 2x – 1 là một đường thẳng đi qua hai điểm là (0; –1) và \(\left(\dfrac{1}{2};0\right)\)
Đồ thị hàm số y = –x + 2 là một đường thẳng đi qua hai điểm là (0; 2) và (2; 0).
Đồ thị của hai hàm số đã cho như hình sau:
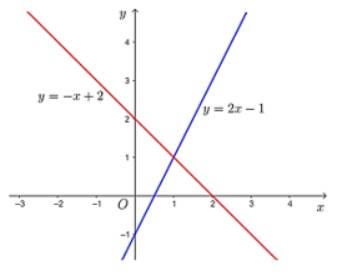
b) Phương trình hoành độ giao điểm của đồ thị hai hàm số là
2x – 1 = –x + 2
3x = 3
x = 1
Thay x = 1 vào hàm số y = 2x – 1, ta được y = 2 . 1 – 1 = 1.
Vậy tọa đô giao điểm của hai đồ thị hàm số trên là điểm A (1; 1).

a)
- Vẽ đồ thị hàm số \(y = x\).
Cho \(x = 1 \Rightarrow y = 1 \Rightarrow \)Đồ thị hàm số đi qua điểm \(M\left( {1;1} \right)\).
Đồ thị hàm số \(y = x\) là đường thẳng đi qua hai điểm \(O\) và \(M\).
- Vẽ đồ thị hàm số \(y = x + 2\)
Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(A\left( {0;2} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 2}}{1} = - 2\) ta được điểm \(B\left( { - 2;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 2\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
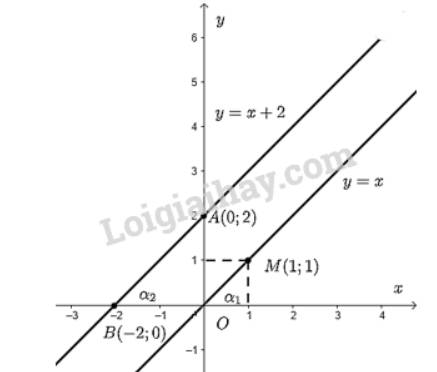
b) Góc tạo bởi hai đường thẳng \(y = x\) và \(y = x + 2\) với trục \(Ox\) lần lượt là \({\alpha _1}\) và \({\alpha _2}\).
Dùng thước đo độ kiểm tra ta thấy số đo \({\alpha _1} = {\alpha _2} = 45^\circ \).

a:Đặt (d1): y=2x-3
Tọa độ giao điểm của (d1) với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=0\end{matrix}\right.\)
Tọa độ giao điểm của (d1) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=2x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0-3=0-3=-3\end{matrix}\right.\)
b: Đặt (d2): \(y=-\dfrac{3}{4}x\)
Tọa độ giao điểm của (d2) với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\-\dfrac{3}{4}x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\)
Tọa độ giao điểm của (d2) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=-\dfrac{3}{4}x=-\dfrac{3}{4}\cdot0=0\end{matrix}\right.\)
c: Đặt \(\left(d3\right):y=2x^2\)
Tọa độ giao điểm của (d3) với trục Ox là:
\(\left\{{}\begin{matrix}2x^2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2=0\\y=2x^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0\\y=2\cdot0^2=0\end{matrix}\right.\)
Tọa độ giao điểm của (d3) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0^2=0\end{matrix}\right.\)
d: Đặt (d4): \(y=\dfrac{x+1}{x-2}\)
ĐKXĐ: x<>2
Tọa độ giao điểm của (d4) với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\y=\dfrac{x+1}{x-2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\)
Tọa độ giao điểm của (d4) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=\dfrac{x+1}{x-2}=\dfrac{0+1}{0-2}=\dfrac{1}{-2}=-\dfrac{1}{2}\end{matrix}\right.\)
e: Đặt (d5): \(y=x-2+\dfrac{1}{x}\)
ĐKXĐ: x<>0
Vì hàm số không đi qua điểm có hoành độ là x=0 nên (d5) sẽ không cắt trục Oy
Tọa độ giao điểm của (d5) với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\x-2+\dfrac{1}{x}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-2x+1=0\\y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x-1\right)^2=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-1=0\\y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
f: Đặt (d6): \(y=x^2+2x-5\)
Tọa độ giao điểm của (d6) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=x^2+2x-5=0^2+2\cdot0-5=-5\end{matrix}\right.\)
Tọa độ giao điểm của (d6) với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\x^2+2x-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x^2+2x+1-6=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\\left(x+1\right)^2=6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}y=0\\x+1=\sqrt{6}\end{matrix}\right.\\\left\{{}\begin{matrix}y=0\\x+1=-\sqrt{6}\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}y=0\\x=\sqrt{6}-1\end{matrix}\right.\\\left\{{}\begin{matrix}y=0\\x=-\sqrt{6}-1\end{matrix}\right.\end{matrix}\right.\)

a: 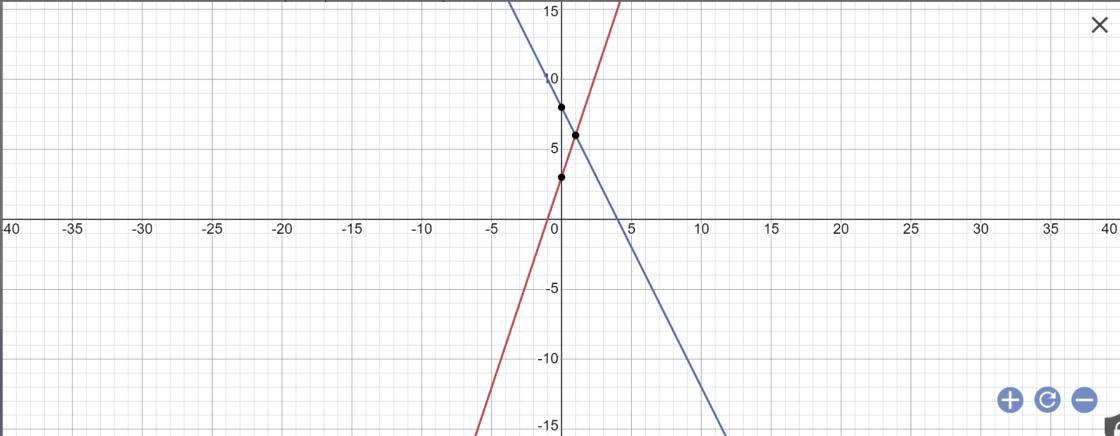
b: Tọa độ A là:
\(\left\{{}\begin{matrix}3x+3=-2x+8\\y=-2x+8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=5\\y=-2x+8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\y=-2+8=6\end{matrix}\right.\)
Vậy: A(1;6)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\3x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+1=0\\y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}y=0\\-2x+8=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-2x=-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\)
Vậy: A(1;6); B(-1;0); C(4;0)
\(AB=\sqrt{\left(-1-1\right)^2+\left(0-6\right)^2}=2\sqrt{10}\)
\(AC=\sqrt{\left(4-1\right)^2+\left(0-6\right)^2}=3\sqrt{5}\)
\(BC=\sqrt{\left(4+1\right)^2+\left(0-0\right)^2}=5\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot BA\cdot AC}=\dfrac{40+45-25}{2\cdot2\sqrt{10}\cdot3\sqrt{5}}=\dfrac{\sqrt{2}}{2}\)
=>\(sinBAC=\sqrt{1-\left(\dfrac{\sqrt{2}}{2}\right)^2}=\dfrac{\sqrt{2}}{2}\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\cdot2\sqrt{10}\cdot3\sqrt{5}=15\)

b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{4}x^2=\dfrac{1}{2}x+2\)
\(\Leftrightarrow x^2-2x-8=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{1}{4}\cdot4^2=4\\y=\dfrac{1}{4}\cdot\left(-2\right)^2=1\end{matrix}\right.\)

a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x=1-3x\\y=2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x=1\\y=2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{5}\\y=\dfrac{2}{5}\end{matrix}\right.\)
b: Thay x=1/5 và y=2/5 vào y=kx+1, ta được:
1/5k+1=2/5
=>1/5k=-3/5
hay k=-3

a) * Vẽ đồ thị hàm số \(y = - \dfrac{1}{2}x + 3\)
Cho x = 0 thì y = 3, ta được điểm P(0; 3) thuộc đồ thị hàm số \(y = - \dfrac{1}{2}x + 3\)
Cho y = 0 thì x = 6 ta được điểm A(6; 0) thuộc đồ thị hàm số \(y = - \dfrac{1}{2}x + 3\)
Vậy đồ thị hàm số \(y = - \dfrac{1}{2}x + 3\) là đường thẳng đi qua hai điểm P(0; 3) và điểm A(6; 0).
* Vẽ đồ thị hàm số y = 2x – 2
Cho x = 0 thì y = -2 ta được điểm Q(0; -2) thuộc đồ thị hàm số y = 2x – 2
Cho y = 0 thì x = 1 ta được điểm B(1; 0) thuộc đồ thị hàm số y = 2x -2
Vậy đồ thị hàm số y = 2x – 2 là đường thẳng đi qua hai điểm Q(0; -2) và B(1; 0)
b) Ta có: A là giao điểm của đường thẳng \(y = - \dfrac{1}{2}x + 3\) với trục hoành nên \( - \dfrac{1}{2}x + 3 = 0\) suy ra x = 6 nên A(6; 0)
Ta có: B là giao điểm của đường thẳng y = 2x – 2 với trục hoành nên 2x – 2 = 0 suy ra x = 1 nên B(1; 0)
Xét phương trình hoành độ giao điểm của hai đường thẳng \(y = - \dfrac{1}{2}x + 3\) và y = 2x – 2 ta có:
\(\begin{array}{l} - \dfrac{1}{2}x + 3 = 2{\rm{x}} - 2\\ \Rightarrow 3 + 2 = \dfrac{1}{2}x + 2{\rm{x}}\\ \Rightarrow 5 = \dfrac{5}{2}x\\ \Rightarrow x = 2 \Rightarrow y = 2\end{array}\)
Vì C là hoành độ giao điểm của hai đường thẳng \(y = - \dfrac{1}{2}x + 3\) và y = 2x – 2 nên C(2; 2)
Gọi H là hình chiếu của C lên trục Ox
Khi đó: CH = 2
Mặt khác AB = 5 cm
Diện tích tam giác ABC là; \({S_{ABC}} = \dfrac{1}{2}CH.AB = \dfrac{1}{2}.2.5 = 5\left( {c{m^2}} \right)\)
mặt phẳng tọa độ Oxy, đồ thị hàm số y = 3/2x - 2 (1) và y = -1/2x + 2 (2). Gọi M là giao điểm của 2 hai đồ thị trên, tìm tọa độ của M
phương trình hoành độ giao điểmM là
3/2x-2=-1/2x+2=>x=2
Tung độ giao điểm M là
y=-1/2.2+2=1
=>M(2;1)
tìm m để đt (d) y= (m-1)x+1 đồng quy với 2 đths (1) và (2)
đt (d) y= (m-1)x+1 đồng quy với 2 đths (1) và (2)
=>đt (d) y= (m-1)x+1 đi qua điểm M(2;1)
=>1=(m-1)2+1=>m=1
sai ròi chắc lun