NT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
3 tháng 1 2017
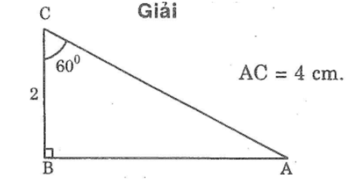
+ Vẽ tam giác ABC:
-) Vẽ đoạn thẳng BC = 2 cm.
-) Trên cùng một nửa mặt phăng bờ BC, vẽ các tia Bx và Cy sao cho ∠CBx = 90º và &BCy = 60º.
Hai tia trên cắt nhau tại A ta được tam giác ABC.
+) Đo AC ta được: AC = 4cm.
PT
1
CM
20 tháng 4 2017
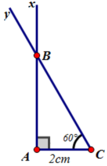
Cách vẽ:
- Vẽ đoạn thẳng AC = 2cm
- Trên cùng một nửa mặt phẳng bờ AC vẽ các tia Ax và Cy sao cho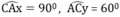 
Hai tia cắt nhau tại B. Ta được tam giác ABC cần vẽ.
ND
0
NT
1
24 tháng 7 2018
A B C H 60
Xét tam giác ABC vuông tại A
Ta có \(\widehat{BAC}=90^o\)(GT)
\(\Rightarrow\widehat{ABC}+\widehat{ACB}=90^o\)( hai góc bù nhau )
Mà \(\widehat{ABC}=60^o\)(GT)
\(\Rightarrow\widehat{ACB}=30^o\)( Bù nhau )
Xét tam giác AHC vuông tại H ta có :
\(\widehat{ACH}=30^o\)(CMT)
\(\Rightarrow\widehat{ACH}+\widehat{HAC}=90^o\)( hai góc bù nhau )
\(\Rightarrow30^o+\widehat{HAC}=90^o\)
\(\Rightarrow\widehat{HAC}=60^o\)
Vì \(\widehat{ABC}=60^o\left(gt\right)\)
Có \(\widehat{HAC}=60^o\left(cmt\right)\)
\(\Rightarrow\widehat{ABC}=\widehat{HAC}=60^o\)
HV
1
AH
Akai Haruma
Giáo viên
29 tháng 6 2023
Lời giải:
Theo BĐT tam giác thì:
$AC< AB+AC$ hay $AC< 9$
$BC< AB+AC$ hay $7< 2+AC$ hay $AC>5$ (cm)
Vậy $9> AC> 5$. Mà $AC$ là số nguyên tố nên $AC=7$
6 tháng 3 2022
a: Xét ΔABD vuông tại A và ΔABC vuông tại A có
AD=AC
AB chung
Do đó: ΔABD=ΔABC
b: Ta có: ΔABD=ΔABC
nên BD=BC
=>ΔBCD cân tại B
mà \(\widehat{C}=60^0\)
nên ΔCBD đều
DN
2
3 tháng 4 2020
tam giác ABC có : ^A + ^B + ^C = 180 (đl) mà ^A = 45; ^C = 70 (gt)
=> ^B = 65
LT
3 tháng 4 2020
tam giác ABC có:
\(\widehat{A}\)+\(\widehat{B}\) +\(\widehat{C}\) = 180
hay 45+B^+70=180
=> B^=180-(45+70)=65
B A C 2cm 60
Ta có : \(\widehat{BAC}+\widehat{ABC}+\widehat{BCA}=180^o\)
\(\Leftrightarrow\widehat{BAC}+90^o+60^o=180^o\)
\(\Leftrightarrow\widehat{BAC}=30^o\)
Xét \(\Delta ABC\)vuông tại B có \(\widehat{BAC}=30^o\)
\(\Rightarrow BC=\frac{1}{2}AC\Leftrightarrow AC=2BC\)
\(\Leftrightarrow AC=2.2=4\left(cm\right)\)
( * ghi nhớ : trong tam giác vuông cạnh đối diện vs góc 30 độ bằng nửa cạnh huyền )
Vậy ...
cảm ơn bạn nhiều