Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
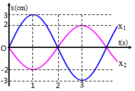
Từ đồ thị ta viết được phương trình dao động của hai vật:
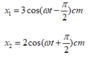
Sử dụng máy tính cộng số phức ta được phương trình của dao động tổng hợp là:
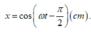
Các đáp án đều cho biết ω = π/2 rad/s. Hoặc có thể dựa vào trục thời gian để xác định chu kì => tần số góc.

Đáp án D
*Từ đồ thị ta nhận thấy hai dao động ngược pha nhau. Lúc t = 0 pha của dao động 1 đi qua vị trí cân bằng theo chiều dương còn pha của dao động 2 đi qua vị trí cân bằng theo chiều âm.
Độ lệch pha: ![]()
Bình luận: Đối với bài toán này ta không quan tâm đến tần số góc bởi vì các đáp án đều có chung tần số góc.

Chọn đáp án D
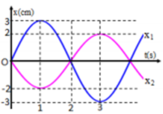
Từ đồ thị ta viết được phương trình dao động của hai vật:
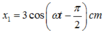
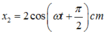
Sử dụng máy tính cộng số phức ta được phương trình của dao động tổng hợp là:
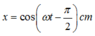
Các đáp án đều cho biết ω = π / 2 rad/s. Hoặc có thể dựa vào trục thời gian để xác định chu kì => tần số góc.

Đáp án D
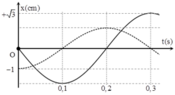
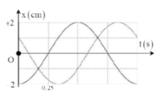
+ Từ đồ thị, ta có 0,25T=0,25s =>T =1(s) ⇒ ω = 2 rad / s
+ Phương trình dao động thành phần
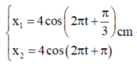
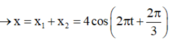

Đáp án B
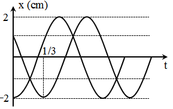
Dễ dàng có được w = 2p rad/s Þ T = 1 s Þ 1/3 = T/3.
Phương trình dao động 1 (li độ x = -2 cm tại t = 0) là: x = -2cos(2pt + p) cm.
Sau khoảng thời gian T/3 thì dao động 2 về đến biên âm Þ tại t = 0, li độ x2 = 1 cm.
Suy ra phương trình x2 = 2cos(2pt + p/3) Þ x = x1 + x2 = 2cos(2pt + 2p/3) cm là phương trình tổng hợp.

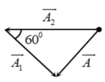
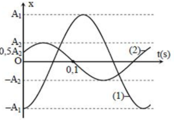
+ Xét đồ thị của A 2 ta thấy tại t = 0 vật ở vị trí x = 0 , 5 A 2 và đang đi lên nên có φ 02 = − π 3
® Góc quét được của vật 2 từ t = 0 đến khi x = 0 là φ = 5 π 6 và mất t = 0 , 1 s
® ω = 5 π 6.0 , 1 = 25 π 3
+ Phương trình dao động của 2 vật là: x 1 = A 1 cos 25 π 3 t − π x 2 = A 2 cos 25 π 3 t − π 3
+ Để A 1 max thì A phải vuông góc với A 2
+ tan π 3 = A A 2 ® A 2 = A tan π 3 = 10 3 3 = 10 cm
® Phương trình vật 2 là: x 2 = 10 cos 25 π 3 t − π 3
Đáp án B


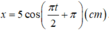
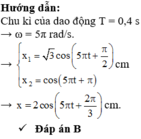
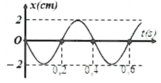
Chu kì T = 4s suy ra: \(\omega=2\pi/T=\pi/2(rad/s)\)
Biên độ A1 = 3cm, ban đầu dao động (1) qua VTCB theo chiều dương, suy ra:
\(x_1=3\cos(\dfrac{\pi}{2}t-\dfrac{\pi}{2})\)
Biên độ A2 = 2cm, ban đầu dao động (2) qua VTCB theo chiều âm, suy ra:
\(x_2=2\cos(\dfrac{\pi}{2}t+\dfrac{\pi}{2})\)
Dao động tổng hợp:
\(x=x_1+x_2=\cos(\dfrac{\pi}{2}t-\dfrac{\pi}{2})\) (cm)