Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn tham khảo link này nha:https://hoc24.vn/hoi-dap/tim-kiem?id=137279&q=Ch%E1%BB%A9ng%20minh%20%3A%20trong%20m%E1%BB%99t%20tam%20gi%C3%A1c%20c%C3%A2n%2C%20%C4%91%C6%B0%E1%BB%9Dng%20ph%C3%A2n%20gi%C3%A1c%20xu%E1%BA%A5t%20ph%C3%A1t%20t%E1%BB%AB%20%C4%91%E1%BB%89nh%20%C4%91%E1%BB%93ng%20th%E1%BB%9Di%20l%C3%A0%20%C4%91%C6%B0%E1%BB%9Dng%20trung%20tuy%E1%BA%BFn%20%E1%BB%A9ng%20v%E1%BB%9Bi%20c%E1%BA%A1nh%20%C4%91%C3%A1y.

Hướng dẫn:
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên
AH ⊥ BC và HB = HC
Xét hai tam giác vuông HAB và HAC có:
HB = HC
ˆH1=ˆH2H1^=H2^ = 900
AH: cạnh chung
Nên ∆HAB = ∆HAC => AB = AC
Vậy ∆ABC cân tại A
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên
AH ⊥ BC và HB = HC

Xét hai tam giác vuông HAB và HAC có:
HB = HC
ˆH1=ˆH2H1^=H2^ = 900
AH: cạnh chung
Nên ∆HAB = ∆HAC => AB = AC
Vậy ∆ABC cân tại A

Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên
AH ⊥ BC và HB = HC
Xét hai tam giác vuông HAB và HAC có:
HB = HC
= 900
AH: cạnh chung
Nên ∆HAB = ∆HAC => AB = AC
Vậy ∆ABC cân tại A
xét tam giác AMB và tam giác AMC, có:
AB=AC
MB=MC(gt)
AM chung
=>tam giác AMB= tam giác AMC (c.c.c)
M1=M2 mà góc M1+góc M2=180 độ
=>góc M1= góc M2= góc MC=90 độ
=>AM vuông góc với BC
mà MA=MB
=>AM là đường trung trực của tam giác ABC
Yên tâm đi chắc chắn đúng

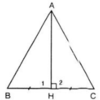
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên AH ⊥ BC và HB = HC
Xét hai tam giác vuông HAB và HAC, có:
HB = HC
AH: cạnh chung
Nên ∆HAB = ∆HAC (hai cạnh góc vuông)
⇒ AB = AC (hai cạnh tương ứng)
Vậy ∆ABC cân tại A.

Câu 1 : ( mình đặt cho dễ viết nha )
Vì \(\Delta\)ABC vuông tại A ( gt )
=> \(\widehat{ABC}+\widehat{ACB}=90^o\)( vì trong tam giác vuông hai góc nhọn phụ nhau )
=> \(\hept{\begin{cases}\widehat{ABC}=90^o-\widehat{ACB}\\\widehat{ACB}=90^o-\widehat{ABC}\end{cases}}\)mà ABC , ACB > 0
=> 90o > ACB , 90o > ABC
hay BAC > ACB , BAC > ABC
Xét tam giác abc có BAC > ACB , BAC > ABC ( CMt )
=> BC là cạnh lớn nhất trong tam giác ( quan hệ giữa góc và cạnh đối diện trong tam giác ) ( dpcm )
Cạnh đối diện với góc vuông gọi là cạnh huyền. Hai cạnh kề với góc vuông là cạnh bên (hay còn gọi là cạnh góc vuông). Cạnh a có thể xem là kề với góc B và đối góc A, trong khi cạnh b kề góc A và đối góc B.
Nếu chiều dài của ba cạnh là các số nguyên, tam giác được gọi là tam giác Pythagore và chiều dài ba cạnh của nó được gọi chung là Bộ ba số Pythagore.
Ví dụ nè tam giác ABC vuông tại A nha
=) góc A = 90 độ
Vì tam giác ABC vuông tại A
=) góc B + góc C = 90 độ
=) góc A > góc B và góc A > góc C
=) góc A là góc lớn nhất
=) BC là cạnh lớn nhất ( ...... )

Thử coi, chả biết đúng không. Không đúng cho t xin lỗi nha
A B C M
Giả dụ đề: Cho tam giác ABC có AM vừa là trung tuyến vừa là đường trung trực
Chứng minh: tam giác ABM = tam giác ACM
Xét tam giác ABM và tam giác ACM có:
\(\hept{\begin{cases}BM=CM\left(gt\right)\\AM:chung\\\widehat{AMB}=\widehat{AMC}=90^0\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.g.c\right)\)
\(\Rightarrow AB=AC\)(hai cạnh tương ứng)
\(\Rightarrow\Delta ABC\)cân tại \(A\)
hay:
\(\Rightarrow\widehat{ABM}=\widehat{ACM}\)(hai góc tương ứng)
\(\Rightarrow\Delta ABC\)cân tại \(A\)
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên AH \(\perp\)BC và HB = HC
Xét 2 tam giác vuông HAB và HAC ta có
HB = HC
\(\widehat{H_1}\)= \(\widehat{H_2}\)= 900
AH : cạnh chung
Nên \(\Delta HAB\)=\(\Delta HAC\)=> AB = AC
Nên \(\Delta ABC\) cân tại A

cho em giải khác nhé
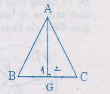
A B C D H G
D thuộc phân giác góc A suy ra DH = DG ( tính chất tia phân giác của một góc )
xét hai tam giác vuông BHD và CGD có
DH = DG ( cmt)
DB = DC ( gt)
do đó tam giác BHD = tam giác CGD ( cạnh huyền - góc nhọn )
suy ra góc B = góc C ( 2 góc tương ứng )
tam giác ABC có góc B = góc C suy ra tam giác ABC cân tại A
Giả sử ∆ABC có AD là phân giác ˆBACBAC^ và DB = DC, ta chứng minh ∆ABC cân tại A
Kéo dài AD một đoạn DA1 = AD

Ta có: ∆ADC = ∆A1DC (c.g.c)
Nên ˆBAD=ˆCA1DBAD^=CA1D^
mà ˆBAD=ˆCADBAD^=CAD^ (gt)
=> ˆCAD=ˆCA1DCAD^=CA1D^
=> ∆ACA1 cân tại C
Ta lại có: AB = A1C ( ∆ADB = ∆A1DC)
AC = A1C ( ∆ACA1 cân tại C)
=> AB = AC
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân
vì AI là đường trung trực nên AI vuông góc với BC và I là trung điểm cuả BC
xét 2 tam giác vuông ABI và tam giác vuông ACI có;
IA chung
góc BAI=gócCAI (do AI là phân giác)
do đó tam giác BAI =tam giác CAI
suy ra AB=AC (2 cạnh tương ứng)
suy ra tam giác ABC cân tại A (định nghĩa tam giác cân)