Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Cứ ba điểm vẽ được 1 tam giác.Vì vậy có thể vẽ được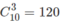 
tam giác.
b) Số đa giác vẽ được là tổng cộng của số tam giác, tứ giác, ngũ giác, …, thập giác.
Do đó vẽ được số đa giác là:
tham khảo
Đa giác đều có 20 cạnh thì sẽ có tất cả 10 đường chéo đi qua tâm của đa giác.
Một hình chữ nhật được tạo thành từ 2 đường chéo đi qua tâm, suy ra số hình chữ nhật được tạo thành là C210C102
Hình vuông được tạo thành từ 2 đường chéo vuông góc nhau, ta có tất cả 5 cặp đường chéo vuông góc nhau, suy ra có tất cả 5 hình vuông.
Vậy có 40 hình chữ nhật (không phải hình vuông) được tạo thành.
Đáp án B.
Số tam giác có 3 đỉnh là 3 trong 15 điểm đã cho bằng số cách chọn 3 điểm trong 15 điểm đã cho và bằng 
(không quan tâm đến thứ tự đỉnh)
Số tam giác lập được thuộc vào một trong hai loại sau
Loại 1: Gồm hai đỉnh thuộc vào a và một đỉnh thuộc vào b
Số cách chọn bộ hai điểm trong 10 thuộc a: 
Số cách chọn một điểm trong 15 điểm thuộc b: 
Loại này có: 
tam giác.
Loại 2: Gồm một đỉnh thuộc vào a và hai đỉnh thuộc vào b
Số cách chọn một điểm trong 10 thuộc a: 
Số cách chọn bộ hai điểm trong 15 điểm thuộc b: 
Loại này có: 
Vậy có tất cả: 
tam giác thỏa yêu cầu bài toán
Chọn C.
Tham khảo:
a)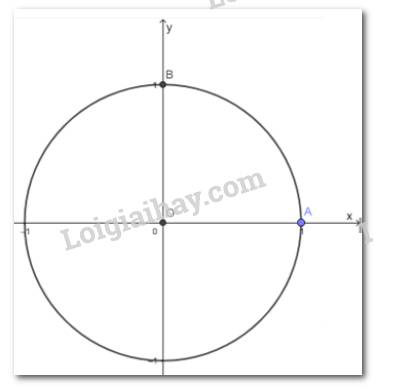 
Góc lượng giác \(\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}\)
b)
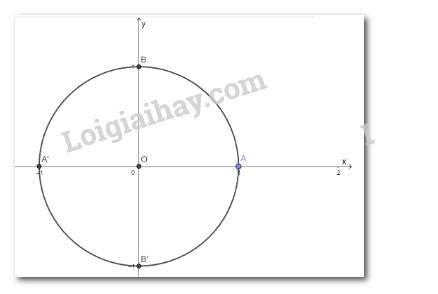
a) Cứ ba điểm vẽ được 1 tam giác. Vì vậy có thể vẽ được \(C^3_{10}=120\) tam giác
b) Số đa giác vẽ được là tổng cộng của số tam giác, tứ giác, ngũ giác,..., thập giác.
Do đó vẽ được \(C^3_{10}+C^4_{10}+C^5_{10}+C^6_{10}+C^7_{10}+C^8_{10}+C^9_{10}+C^{10}_{10}=968\) đa giác