Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Một khối gỗ gồm đế là hình lập phương cạnh 9 cm và một hình chóp tứ giác đều. Tính thể tích khối gỗ.
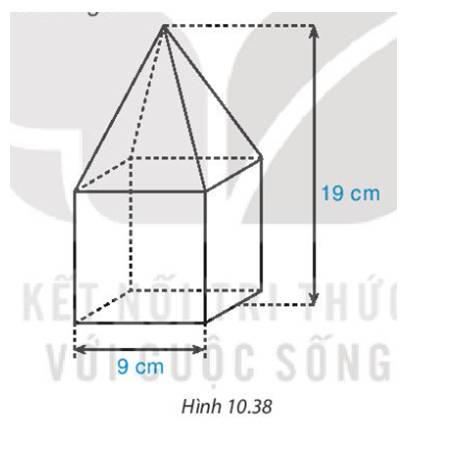

Có chiều cao của cả khối gỗ là 9 cm, chiều cao cụa hình lập phương là 9 cm
=> Chiều cao của hình chóp tứ giác đều là: 19−9=10 (cm)
- Diện tích mặt đáy của hình chóp tứ giác đều là: 9.9=81 (cm2)
- Thể tích hình chóp là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.81.10 = 270\left( {c{m^3}} \right)\)
- Thể tích hình lập phương là: V=9.9.9=729 \(\left( {c{m^3}} \right)\)
Vậy thể tích của khối gỗ là: 270+729= 999 (cm3)

Thể tích của khối gỗ hình lập phương là:
\( V_{lp} = 30^3 = 27000 (cm^3)\)
Thể tích vật thể có hình chóp tứ giác đều là:
\(V_{hc} = \frac{1}{3}.30^2.30 = 9000 (cm^3)\)
Thể tích phần khúc gỗ bị cắt bỏ là:
\( V = V_{lp} - V_{hc} = 27000 - 9000 = 18000 (cm^3)\)
Vậy thể tích của phần khúc gỗ đã bị cắt bỏ là \(18000 cm^3\)

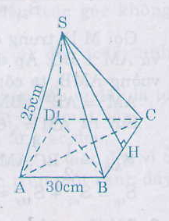
Ta có : \(d=SH=\sqrt{SB^2-BH^2}\)
\(=\sqrt{25^2-15^2}=\sqrt{400}=20\left(cm\right)\)
Diện tích xung quanh của hình chóp:
Sxq = pd = \(\dfrac{1}{2}\).30.4.20 = 1200 (cm2)
Diện tích đáy: Sđ = 302 = 900(cm2)
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sđ = 1200 + 900 = 2100(cm2)

a: O ở đâu vậy bạn?
b: Diện tích đáy là \(6.5^2=42.25\left(cm^2\right)\)
Thể tích hình chóp là: \(V=\dfrac{1}{3}\cdot42.25\cdot12=169\left(cm^3\right)\)

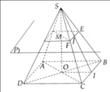
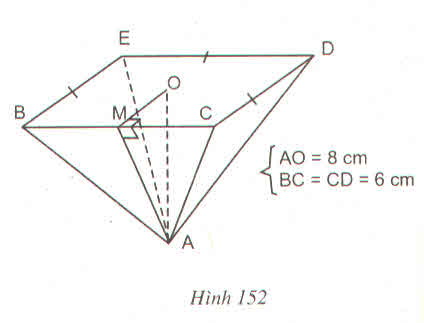
a) Gọi O là tâm của đáy ABCD, M là giao điểm của SO và mặt phẳng (P). Ta có: OM = 2(cm).
Ta tính được O B = 2 2 c m rồi suy ra SO = 5 (cm)
Từ đó chiều cao cần tìm là: SM = SO - OM 3 (cm)
b) Gọi I là trung điểm của BC. E, F, J lần lượt là giao điểm của SB, SC, SI với mặt phẳng (p).
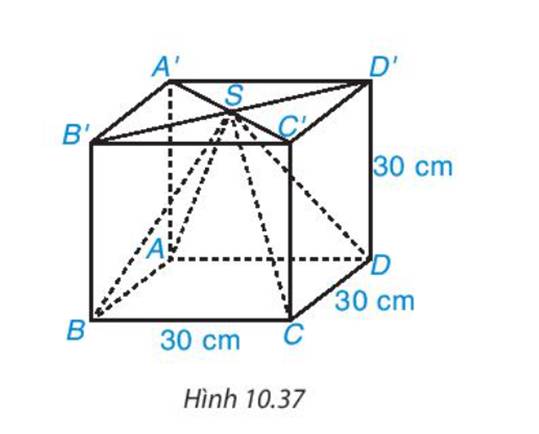


Diện tích mặt đáy của hình chóp tứ giác đều ABCD là: 30.30=900 (cm2)
- Thể tích hình chóp là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.900.30 = 9000(c{m^3})\)
- Thể tích hình lập phương là V=30.30.30=27000 (cm3)
Vậy thể tích phần gỗ bị cắt đi là V = 27000 − 9000=18000 (cm3)