Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

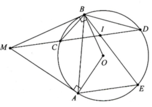
a, Vì M B C ^ = M D B ^ = 1 2 s đ C B ⏜ nên chứng minh được ∆MBC:∆MDB (g.g)
b, Vì
M
B
O
^
+
M
A
O
^
=
180
0
nên tứ giác MAOB nội tiếp
c, Đường tròn đường kính OM là đường tròn ngoại tiếp tứ giác MAOB => r = M O 2
Gọi H là giao điểm của AB với OM
=> OH ⊥ AB; AH = BH = R 3 2
Giải tam giác vuông OAM, đường cao AH ta được OM = 2R Þ r = R
d, Ta có M I B ^ = s đ D E ⏜ + s đ B C ⏜ 2 và M A B ^ = s đ A C ⏜ + s đ B C ⏜ 2
Vì AE song song CD => s đ D E ⏜ = s đ A C ⏜ => M I B ^ = M A B ^
Do tứ giác MAIB nội tiếp hay 5 điểm A, B, O, I, M nằm trên cùng 1 đường tròn kính MO
Từ đó ta có được M I O ^ = 90 0 => OI ⊥ CD hay I là trung điểm của CD

a)
MA và MB là các tiếp tuyến của (O)
=> OM _I_ AB mà C thuộc OM
=> AC = BC
OB = OA = OC = OD ( = R)
=> \(\Delta ACD\) vuông tại A và \(\Delta BCD\) vuông tại B
\(\Rightarrow\Delta ACD=\Delta BCD\left(ch-cgv\right)\)
\(\Rightarrow\Delta ACD~\Delta BCD\)
\(\Rightarrow\frac{AC}{BC}=\frac{AD}{BD}\)
\(\Rightarrow AC\times BD=AD\times BC\left(\text{đ}pcm\right)\)
b)
AI là đpg của \(\Delta ACD\)
\(\Rightarrow\frac{IC}{ID}=\frac{AC}{AD}\) mà \(\frac{AC}{AD}=\frac{BC}{BD}\)
\(\Rightarrow\frac{IC}{ID}=\frac{BC}{BD}\)
=> BI là đpg của \(\Delta BCD\) (đpcm)
a) MA và MB là các tiếp tuyến của (O)
=> OM _I_ AB mà C thuộc OM
=> AC = BC
OB = OA = OC = OD ( = R)
=> \Delta ACDΔACD vuông tại A và \Delta BCDΔBCD vuông tại B
\Rightarrow\Delta ACD=\Delta BCD\left(ch-cgv\right)⇒ΔACD=ΔBCD(ch−cgv)
\Rightarrow\Delta ACD~\Delta BCD⇒ΔACD ΔBCD
\Rightarrow\frac{AC}{BC}=\frac{AD}{BD}⇒BCAC=BDAD
\Rightarrow AC\times BD=AD\times BC\left(\text{đ}pcm\right)⇒AC×BD=AD×BC(đpcm)
b)
AI là đpg của \Delta ACDΔACD
\Rightarrow\frac{IC}{ID}=\frac{AC}{AD}⇒IDIC=ADAC mà \frac{AC}{AD}=\frac{BC}{BD}ADAC=BDBC
\Rightarrow\frac{IC}{ID}=\frac{BC}{BD}⇒IDIC=BDBC
=> BI là đpg của \Delta BCDΔBCD (đpcm)


1) Xét (O) có
\(\widehat{CAB}\) là góc nội tiếp chắn \(\stackrel\frown{CB}\)
\(\widehat{BCM}\) là góc tạo bởi tiếp tuyến CM và dây cung CB
Do đó: \(\widehat{CAB}=\widehat{BCM}\)(hệ quả)
\(\Leftrightarrow\widehat{MCB}=\widehat{MAC}\)
Xét ΔMBC và ΔMCA có
\(\widehat{MCB}=\widehat{MAC}\)(cmt)
\(\widehat{AMC}\) chung
Do đó: ΔMBC∼ΔMCA(g-g)
Suy ra: \(\dfrac{MB}{MC}=\dfrac{MC}{MA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(MC^2=MB\cdot MA\)(đpcm)
Em cần viết đề bài rõ ràng hơn, các điểm cần viết hoa nhé