

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



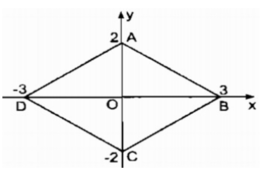
Ta có: A(0;2) và C(0;-2) là hai điểm đối xứng qua O(0;0)
⇒ OA = OC
B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)
⇒ OB = OD
Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Lại có: Ox ⊥ Oy hay AC ⊥ BD.
Vậy tứ giác ABCD là hình thoi
Trong ∆ OAB vuông tại O, theo định lý Pi-ta-go ta có:
A B 2 = O A 2 + O B 2
A B 2 = 2 2 + 3 2 = 4 + 9 = 13
AB = 13
Vậy chu vi của hình thoi bằng 4 13

\(A\left( { - 2;0} \right)\) \( \Rightarrow \) hoành độ của điểm \(A\) là –2 và tung độ của điểm \(A\) là 0.
\(B\left( {0;4} \right)\) \( \Rightarrow \) hoành độ của điểm \(B\) là 0 và tung độ của điểm \(B\) là 4.
\(C\left( {5;4} \right)\) \( \Rightarrow \) hoành độ của điểm \(C\) là 5 và tung độ của điểm \(C\) là 4.
\(D\left( {3;0} \right)\) \( \Rightarrow \) hoành độ của điểm \(D\) là 3 và tung độ của điểm \(D\) là 0.
Biểu diễn các điểm \(A;B;C;D\) trên mặt phẳng tọa độ ta được:
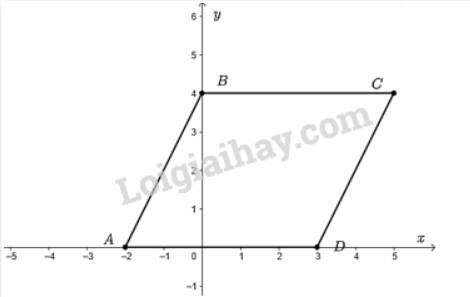
Vì hai điểm \(B;C\) có tung độ bằng nhau nên \(BC\) song song với \(Ox\); Hai điểm \(A;D\) có tung độ bằng nhau nên \(AD\) song song với \(Ox\).
Do đó, \(BC//AD\).
Lại có, \(AD = \left| {3 - \left( { - 1} \right)} \right| = 4;BC = \left| {4 - 0} \right| = 4\). Do đó, \(AD = BC\).
Xét tứ giác \(ABCD\)có:
\(AD = BC\)
\(BC//AD\)
Do đó, tứ giác \(ABCD\) là hình bình hành.

a) \(a^2+b^2+c^2+d^2=ab+bc+ac+cd.\)
<=>\(2a^2+2b^2+2c^2+2d^2=2ab+2ac+2bc+2cd\)
<=>\(2a^2+2b^2+2c^2+2d^2-2ab-2bc-2ac-2cd=0\)
<=>\(\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)+\left(d^2-2cd+c^2\right)\)=0
<=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2+\left(d-c\right)^2=0\)
=>a=b=c=d
=> ABCD là hình thoi

Các bước làm như sau:
- Xác định các điểm A, B, C, D trên hình vẽ với A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).
- Vẽ tứ giác ABCD.
- Vẽ hai đường chéo AC và BD. Gọi K là giao điểm của hai đường chéo đó.
- Xác định tọa độ của điểm K: K(5 ; 6)
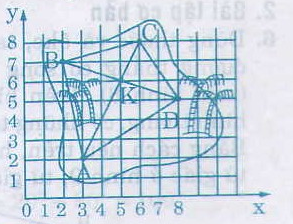
Vậy vị trí kho báu có tọa độ K(5 ; 6) trên hình vẽ.
Bài giải:
Các bước làm như sau:
- Xác định các điểm A, B, C, D trên hình vẽ với A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).
- Vẽ tứ giác ABCD.
- Vẽ hai đường chéo AC và BD. Gọi K là giao điểm của hai đường chéo đó.
- Xác định tọa độ của điểm K: K(5 ; 6)
Vậy vị trí kho báu có tọa độ K(5 ; 6) trên hình vẽ. 

Ta có: A(0;-4) và C(0;4) là hai điểm đối xứng qua O(0;0)
⇒ OA = OC
B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)
⇒ OB = OD
Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Lại có: Ox ⊥ Oy hay AC ⊥ BD.
Vậy tứ giác ABCD là hình thoi
Trong Δ∆OAB vuông tại O, theo định lý Pi-ta-go ta có:
AB2=OA2+OB2
AB2=42+32 = 16 + 9 = 25
AB = √25
Vậy chu vi của hình thoi bằng 4√25

a) phương trình
<=> x \(\in\) Z và x \(\le\) \(\frac{4x+1}{9}\) < x +1 (1)
(1) <=> 0 \(\le\) \(\frac{4x+1}{9}-x\) < 1
<=> 0 \(\le\) 4x + 1 - 9x < 9 <=> 0 \(\le\) 1 - 5x < 9 <=> \(-\frac{9}{5}\) < x \(\le\) \(\frac{1}{5}\)
Mà x nguyên nên x = -1; 0