Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D O I H K C'
+) Chứng minh nếu AD // BC thì đường tròn (I) đường kính CD tiếp xúc AB:
Gọi tiếp điểm giữa (O) và CD là H .Từ I hạ IK vuông góc AB tại K.
Khi đó tứ giác KOHI nội tiếp đường tròn (OI) => ^KHI = ^KHD = ^KOI
Dễ thấy tứ giác ABCD là hình thang (Vì BC // AD) có đường trung bình OI nên OI // BC // AD
=> ^KOI = ^KBC. Do đó ^KHD = ^KBC => Tứ giác BKHC nội tiếp. Tương tự, tứ giác ADHK nội tiếp
Từ đó ^DKC = ^DKH + ^CKH = ^DAH + ^CBH. Kết hợp với AD // BC suy ra ^DKC = ^BHA = 900
=> Điểm K thuộc đường tròn (I). Mà AB vuông góc IK tại K nên (I) tiếp xúc AB (*)
+) Chứng minh nếu (I) đường kính CD tiếp xúc với AB thì AD // BC:
Ta gọi tiếp điểm giữa (I) và AB là K, qua K kẻ đường thẳng song song với AH cắt CD tại C'
Lúc này, ^KC'I = ^AHD = ^ABH. Ta có KC' // AH; AH vuông góc BH => KC' vuông góc BH
Do KI vuông góc AB nên ^IKC' = ^ABH. Suy ra ^KC'I = ^IKC' => \(\Delta\)KIC' cân tại I
=> IC' = IK = IC. Mà C và C' nằm cùng phía so với IK nên C trùng C'.
Từ đây ^KCH = ^AHI = ^KBH => Tứ giác KHCB nội tiếp. Hoàn toàn tương tự, tứ giác AKHD nội tiếp
Vậy thì ^HCB = ^HKA = 1800 - ^ADH => AD // BC (**)
+) Qua (*) và (**), ta thu được ĐPCM.

bn tựu vẽ hk nha
a, dễ cm tứ giác ABCD là hình thang
ta có AD//MO//CB(cùng vuông góc vs DC)
A0=B0
từ đây suy ra DM=MC
B, TỪ M KẺ MH VUÔNG GÓC VS AB
TA CÓ GÓC DAM=GÓC AMO( do AD//MO) (1)
LẠI CÓ GÓC AMO=GÓC MAO( do MO=AO) (2)
TỪ (1)(2) SUY RA GÓC DAM=GÓC MAO
LẠI CÓ GÓC D=GÓC MHA=90
SUY RA TAM GIAC DMA=TAM GIAC HMA
SUY RA AD=AH
tự BC=HB
TỪ ĐÂY SUY RA AD+CB=AH+BH=AB KO ĐỔI
C, TA CÓ MH=DM=MC(CMT)
LẠI CÓ MHVUOONG GÓC VS AB
SUY RA DƯỜNG TRÒN CD TX VS AB
D, TRONG HT VUÔNG ABCD CÓ DC<=AB
SUY RA SABCD=\(\frac{\left(AD+CB\right).DC}{2}=\frac{AB.CD}{2}< =\frac{AB^2}{2}\)
DẤU = XẢY RA KHI M NẰM CHÍNH GIỬA CUNG AB

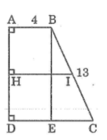
Gọi I là trung điểm của BC
Ta có: IB = IC = (1/2).BC = (1/2).13 = 6,5 (cm) (1)
Kẻ IH ⊥ AD. Khi đó HI là đường trung bình của hình thang ABCD.
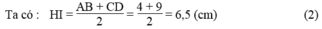
Từ (1) và (2) suy ra : IB = IH = R
Vậy đường tròn (I ; BC/2 ) tiếp xúc với đường thẳng AD

Lời giải:
Gọi giao của $BO$ và $AC$ là $H$
Vì $BA=BC; OA=OC$ nên $BO$ là trung trực của $AC$
$\Rightarrow BO$ vuông góc với $AC$ tại trung điểm $H$ của $AC$.
Do đó $HO$ là đường trung bình ứng với cạnh $CD$ của tam giác $ACD$
$\Rightarrow HO=2$
$BH=BO-HO=R-2$
Theo định lý Pitago:
$BC^2-BH^2=CH^2=CO^2-HO^2$
$\Leftrightarrow (4\sqrt{3})^2-(R-2)^2=R^2-2^2$
$\Leftrightarrow 48-(R-2)^2=R^2-4$
$\Rightarrow R=6$ (cm)
