TT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TA
1
ND
15 tháng 6 2019
Gọi O là giao điểm 2 đường chéo của tứ giác ABCD.
Xét :Tam giác BOC có: BC < OB + OC (bất đẳng thức trong tam giác)
Tam giác AOD có: AD < OD + OA (.............................................)
Do đó: BC + AD < (OB + OD) +(OC + OA)
hay BC + AD < BD + AC
Mà AD = AC (GT) => BC < BD.
A B C D O
CD
0
CD
0
TH
0
SY
1
9 tháng 6 2017
Bạn tự vẽ hình nhá :)
Gọi O là giao điểm 2 đường chéo.
Tam giác BOC có:BC < OB + OC
Tam giác AOD có: AD < OD + OA
Do đó: BC + AD < (OB + OD) +(OC + OA)
Hay BC + AD < BD + AC
Mà AD = AC => BC < BD
(đ.p.c.m)
19 tháng 7 2016
A B C D O
Gọi O là giao điểm hai đường chéo AC và BD
- Xét lần lượt các tam giác OAB , OBC , OCD , OAD và áp dụng bất đẳng thức tam giác được :
\(OA+OB>AB\) ; \(OB+OC>BC\) ; \(OC+OD>CD\) ; \(OA+OD>AD\)
Cộng các bất đẳng thức trên theo vế được : \(2\left(OA+OB+OC+OD\right)>AB+BC+CD+AD\)
\(\Rightarrow2\left(AC+BD\right)>AB+BC+CD+AD\) \(\Rightarrow AC+BD>\frac{AB+BC+CD+DA}{2}\) (1)
- Tương tự, lần lượt xét các tam giác ACD , BCD , BAC , ABD và áp dụng bất đẳng thức tam giác được :
\(AD+CD>AC\) ; \(BC+CD>BD\) ; \(AB+BC>AC\) ; \(AB+AD>BD\)
Cộng các bất đẳng thức trên theo vế được : \(2\left(AC+BD\right)< 2\left(AB+BC+CD+DA\right)\)
\(\Rightarrow AC+BD< AB+BC+CD+DA\)(2)
Từ (1) và (2) ta có : \(\frac{AB+BC+CD+DA}{2}< AC+BD< AB+BC+CD+AD\)
hay \(\frac{AB+BC+CD+DA}{2}< OA+OB+OC+OD< AB+BC+CD+AD\)
27 tháng 9 2019
A B C D O
Theo bất đẳng thức tam giác ta có:
\(OA+OB>AB\)
\(OB+OC>BC\)
\(OC+OD>DC\)
\(OD+OA>AD\)
Cộng vế theo vế thì \(2\left(OA+OB+OC+OD\right)>AB+BC+CA+AD\)
\(\Rightarrow OA+OB+OC+OD>\frac{AB+BC+CA+AD}{2}\) ( 1 )
Theo bất đẳng thức tam giác ta có:
\(AB+BC>CA;BC+CD>BD;CD+DA>CA;DA+AB>BD\)
Cộng vế theo vế ta có:
\(2\left(AB+BC+CD+AD\right)>2\left(CA+BD\right)=2\left(AO+OC+OD+OB\right)\)
\(\Leftrightarrow AB+BC+CD+DA>OA+OB+OC+OD\) ( 2 )
Từ ( 1 ) ; ( 2 ) suy ra đpcm.
CM
10 tháng 12 2017
Vì △ AOD đồng dạng △ BOC nên: ∠ ADO = ∠ BCO hay ∠ EDB = ∠ ECA
Xét △ EDB và △ ECA ta có:
∠ E chung
∠ (EDB) = ∠ (ECA) (chứng minh trên)
Vậy △ EDB đồng dạng △ ECA(g.g)
Suy ra: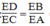
⇒ ED.EA = EC.EB
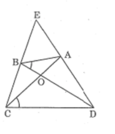
Gọi O là giao điểm của hai đường chéo AC và AD .
Xét \(\Delta AOD\)có :
\(AD< AO+OD\)(1)
Xét \(\Delta BOC\)có :
\(BC< OC+BO\)(2)
tỪ (1) VÀ (2)
Cộng vế với vế ta được :
\(AD+BC< AC+BD\)(3)
Theo đề bài ta có :
\(AC=AD\)
\(\Rightarrow BC< BD\)(đpcm)
O B C A D