Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) C/m tg ABCO nội tiếp:
+) Ta có: góc ACO = 90•( vì AC là tiếp tuyến đg tròn (O))
góc ABO = 90•( vì AB là tiếp tuyến đg tròn (O))
+) Xét tg ABOC có: góc ACO+ góc ABO=90•+90•=180•
Mà 2 góc ở vị trí đối nhau
=> tg ABOC nội tiếp đg tròn(dhnb)
b) C/m: CD// AO:
+) Vì AB và AC là 2 tiếp tuyến cắt nhau tại A(gt) => AO là đg pg của góc COB( t/c 2 tiếp tuyến cắt nhau)
=> AO là pg của tam giác COB
Mà tam giác COB cân tại O( OB=OC=R)
=> OA là đg cao của tam giác COB( t/c tam giác cân)
=> OA vuông góc vs CB( t/c) (1)
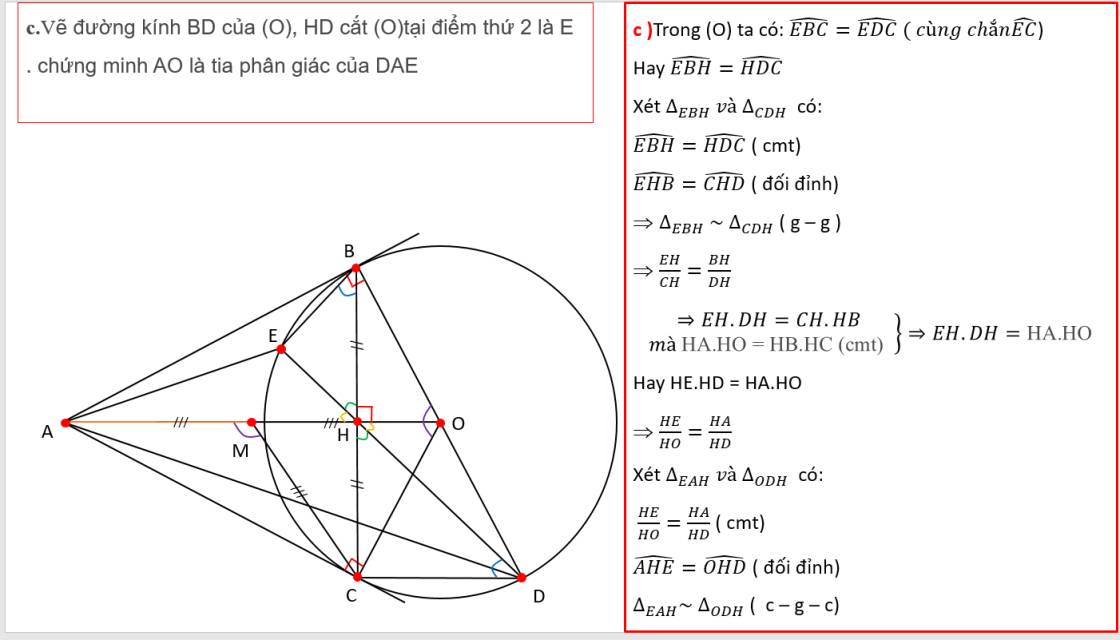
+) Xét (O) ta có:
BD là đg kính( gt)
góc BCD là góc nội tiếp chắn cung BD
=> góc BCD= 90• ( t/c góc nội tiếp chắn nửa đg tròn)
=> CD vuông góc vs CB(t/c) (2)
Từ(1) và (2) suy ra: CD// OA( từ vuông góc đến song song).
mk chưa ra câu c nên xin lỗi bn nhiều nhé....

a) Ta có: \(\angle ABO+\angle ACO=90+90=180\Rightarrow ABOC\) nội tiếp
Vì AB,AC là tiếp tuyến \(\Rightarrow\Delta ABC\) cân tại A và AO là phân giác \(\angle BAC\)
\(\Rightarrow AO\bot BC\)
b) Ta có: \(\angle OME=\angle OBE=90\Rightarrow OMBE\) nội tiếp
\(\Rightarrow\angle OBM=\angle OEM\)
c) Vì \(\Delta ABC\) cân tại A và AO là phân giác \(\angle BAC\)
\(\Rightarrow H\) là trung điểm BC
Tương tự như câu b \(\Rightarrow\angle OFM=\angle OCM\)
mà \(\angle OBM=\angle OCM\) (\(\Delta OBC\) cân tại O)
\(\Rightarrow\angle OFM=\angle OEM\Rightarrow\Delta OFE\) cân tại O có \(OM\bot FE\)
\(\Rightarrow\) M là trung điểm FE
Xét \(\Delta HFM\) và \(\Delta BEM:\) Ta có: \(\left\{{}\begin{matrix}MH=MB\\MF=ME\\\angle HMF=\angle BME\end{matrix}\right.\)
\(\Rightarrow\Delta HFM=\Delta BEM\left(c-g-c\right)\Rightarrow\angle HFM=\angle BEM\)
\(\Rightarrow HF\parallel BE\Rightarrow HF\parallel AB\) mà H là trung điểm BC
\(\Rightarrow F\) là trung điểm BC


a)Vì AB,AC là tt
`=>hat{ABO}=hat{ACO}=90^o`
Xét tg ABOC có:
`hat{ABO}+hat{ACO}=180^o`
Mà đây là 2 góc đối nhau
`=>` tg ABOC nt
Vì AB,AC là 2 tt cắt tại A
`=>AB=AC`
Mà `OB=OC=R`
`=>` AO là trung trực BC
`=>OA bot BC`
`b)` Không có điểm H sao chứng minh?
Bạn ơi, tứ giác A gì á?