Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(AB=\sqrt{OA^2+OB^2}=OA\sqrt{1+k^2}\)
\(OM=BM=\dfrac{1}{2}AB=\dfrac{OA}{2}\sqrt{1+k^2}\)
\(cos\widehat{OMB}=cos60^0=\dfrac{OM^2+BM^2-OB^2}{2OM.BM}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{OA^2\left(\dfrac{k^2+1}{4}\right)+OA^2\left(\dfrac{k^2+1}{4}\right)-k^2OA^2}{2.OA^2\left(\dfrac{k^2+1}{4}\right)}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{1-k^2}{1+k^2}=\dfrac{1}{2}\Rightarrow k^2=\dfrac{1}{3}\Rightarrow k=\dfrac{1}{\sqrt{3}}\)

Gọi N là trung điểm AC \(\Rightarrow MN||AB\Rightarrow\widehat{OMN}\) là góc giữa OM và AB
Đặt \(OA=a\)
\(AB=\sqrt{OA^2+OB^2}=\sqrt{a^2+k^2a^2}=a\sqrt{k^2+1}\)
\(AC=\sqrt{OA^2+OC^2}=a\sqrt{k^2+1}\)
\(BC=\sqrt{OB^2+OC^2}=a.k\sqrt{2}\)
\(MN=\dfrac{1}{2}AB=\dfrac{a}{2}\sqrt{k^2+1}\) ; \(OM=\dfrac{BC}{2}=a.\dfrac{k\sqrt{2}}{2}\) ; \(ON=\dfrac{1}{2}AC=a.\dfrac{\sqrt{k^2+1}}{2}\)
\(cos\widehat{OMN}=cos60^0=\dfrac{OM^2+MN^2-ON^2}{2OM.MN}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{a^2.\dfrac{k^2}{2}}{2.a^2.\dfrac{k\sqrt{2k^2+2}}{4}}=\dfrac{1}{2}\Leftrightarrow2k=\sqrt{2k^2+2}\)
\(\Leftrightarrow4k^2=2k^2+2\Rightarrow k=1\)

Đề bài có vấn đề gì không nhỉ?
Tam giác OAB vuông cân tại O nên OM là trung tuyến đồng thời là đường cao
\(\Rightarrow OM\perp AB\) hay góc giữa OM và AB bằng 90 độ (cosin góc giữa 2 đường thẳng bằng 0)

Do \(d\perp\left(ABC\right)\) nên \(MN\perp BC\)
\(\left\{{}\begin{matrix}MC\perp\left(BOH\right)\\BN\subset\left(BOH\right)\end{matrix}\right.\) \(\Rightarrow MC\perp BN\)
\(\left\{{}\begin{matrix}MB\perp\left(CHO\right)\\CN\subset\left(CHO\right)\end{matrix}\right.\)\(\Rightarrow MB\perp CN\)



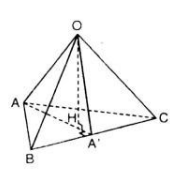

Tam giác OAB vuông tại O (OA ⊥ OB)
Theo định lý Py-ta-go ta có: A B = O A 2 + O B 2 = 1 2 + 1 2 = 2
Tương tự BC = 2
Ta có: OM là trung tuyến của tam giác OAB vuông tại O
Nên OM = 1/2AB = 1 2 . 2 = 2 2
Đáp án D