

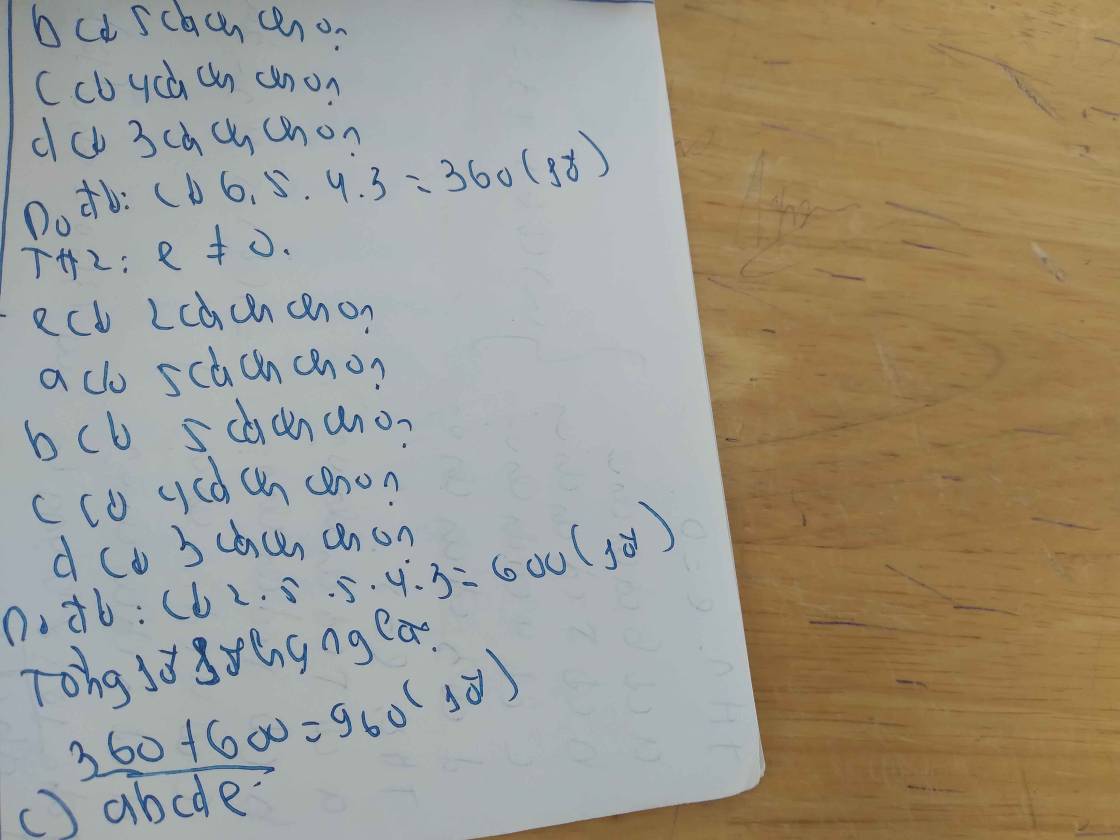


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


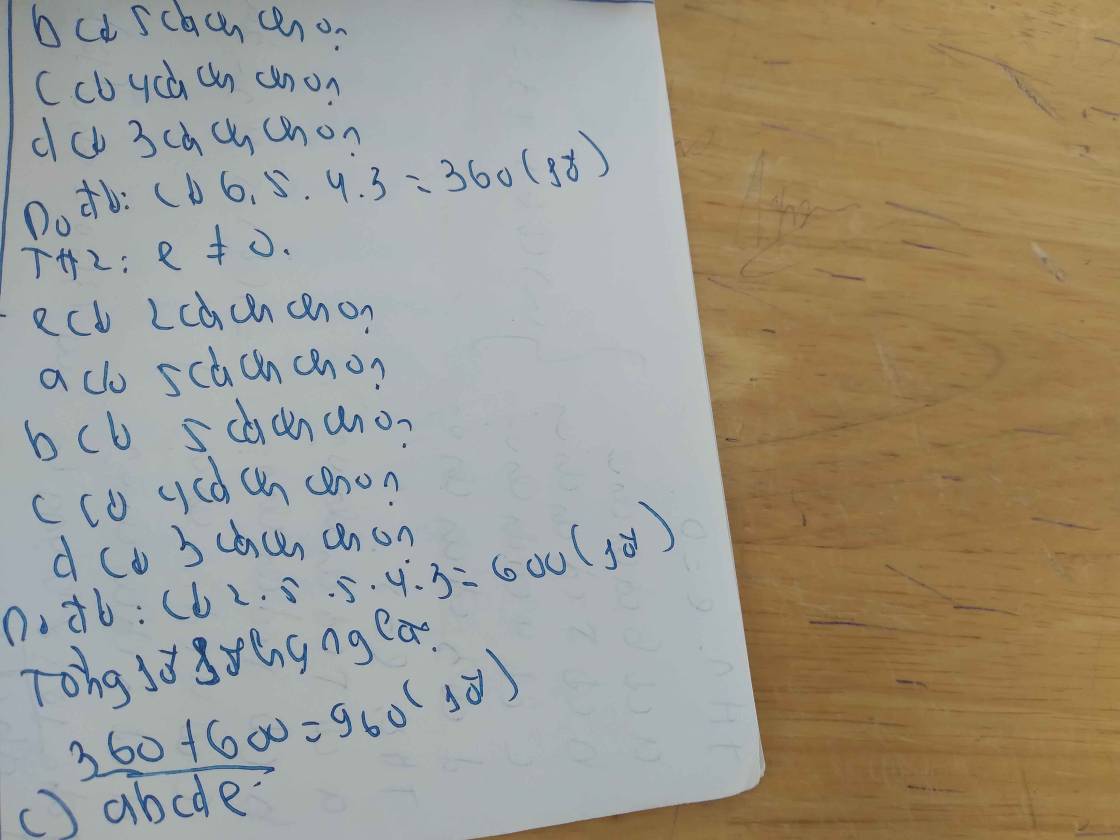



Số bất kì: \(6!-5!\) số
Xếp 0 và 5 cạnh nhau: 2 cách
Hoán vị bộ 05 với 4 chữ số còn lại: \(5!\) cách
Hoán vị bộ 05 với 4 chữ số còn lại sao cho 0 đứng đầu: \(4!\) cách
\(\Rightarrow2.5!-4!\) cách xếp sao cho 0 và 5 cạnh nhau
\(\Rightarrow6!-5!-\left(2.5!-4!\right)\) cách xếp thỏa mãn

\(\overline{abcde}\)
TH1: e=0
e có 1 cách chọn
Chữ số 2 có 4 cách chọn
ba chỗ còn lại có 4*3*2=24 cách
=>Có 4*24=96 cách
TH2: e=5; a=2
a,e có 1 cach
b có 4 cách
c có 3 cách
dcó 2 cách
=>Có 4*3*2=24 cách
TH3: e=5; a<>2
e có 1 cách chọn
a có 3 cách chon
số 2 có 3 cách
hai số còn lại có 3*2=6 cách
=>Có 3*3*6=54 cách
=>CÓ 96+24+54=174 số

Các bộ số có thể là (0;3;6); (0;1;5); (0;4;8); (0;1;8); (0;4;5); (1;3;5); (1;3;8); (1;5;6); (3;4;5); (3;4;8); (4;6;8)
Với các bộ (0;3;6); (0;1;5); (0;4;8); (0;1;8); (0;4;5) thì có thể lập được:
\(2\cdot2\cdot1\cdot5=20\left(số\right)\)
Với các bộ còn lại thì lập được 3!*6=6*6=36 số
=>Có 20+36=56 số

Các số tự nhiên nhỏ hơn 1000 gồm các số có 1 chữ số, có 2 chữ số hoặc 3 chữ số.
+ Số có 1 chữ số chia hết cho 5 là: 0 và 5 => có 2 số.
+ Số có 2 chữ số chia hết cho 5:
Hàng đơn vị là 0: chữ số hàng chục có 9 cách chọn.
Hàng đơn vị là 5: chữ số hàng chục có 8 cách chọn (khác 0).
=> Có \(9 + 8 = 17\) (số)
+ Số có 3 chữ số chia hết cho 5:
Hàng đơn vị là 0: chữ số hàng trăm có 9 cách chọn, hàng chục có 8 cách chọn.
Hàng đơn vị là 5: chữ số hàng trăm có 8 cách chọn, hàng chục có 8 cách chọn.
=> Có 9.8+8.8 = 136 (số)
Vậy có tất cả \(2 + 17 + 136 = 155\) số thỏa mãn ycbt.

a: \(\overline{abcd}\)
a có 7 cách chọn
b có 6 cách
c có 5 cách
d có 4 cách
=>Có 7*6*5*4=840 cách
b: Bộ ba chia hết cho 9 sẽ có thể là (1;2;6); (1;3;5); (2;3;4)
Mỗi bộ có 3!=6(cách)
=>Có 6*3=18 cách
c: \(\overline{abcde}\)
e có 3 cách
a có 6 cách
b có 5 cách
c có 4 cách
d có 3 cách
=>Có 3*6*5*4*3=1080 cách

a, Số các số tự nhiên gồm 8 chữ số đôi một khác nhau được lập từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8 là: \({P_8} = 8! = 40320\)( số )
b, Số các số tự nhiên gồm 6 chữ số đôi một khác nhau được lập từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8 là: \(P_8^6 = 20160\)( số )

Số các số tự nhiên có 5 chữ số khác nhau lập nên từ 5 chữ số này là 5!=120(số)
Số các số tự nhiên có 5 chữ số khác nhau lập nên từ 5 chữ số này có bắt đầu là 34 là: 3!=6(số)
=>Có 120-6=114(số) cần tìm

TH1: chữ số hàng đơn vị là 4, khi đó hàng chục là 5
Chọn 2 chữ số còn lại và xếp vào 2 vị trí đầu có \(A_7^2=42\) cách
TH2: chữ số hàng đơn vị khác 4 \(\Rightarrow\) có 3 cách chọn từ 2, 6, 8
Chọn chữ số còn lại có 6 cách
Hoán vị chữ số đó và cặp 45: \(2!.2!=4\) cách
\(\Rightarrow3.6.4=72\) số
Tổng: \(42+72=114\) số