Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(x\left( t \right) = {x_1}\left( t \right) + {x_2}\left( t \right) = 2\left[ {\cos \left( {\frac{\pi }{3}t + \frac{\pi }{6}} \right) + \cos \left( {\frac{\pi }{3}t - \frac{\pi }{3}} \right)} \right]\)
\(2\left[ {\cos \left( {\frac{{\frac{\pi }{3}t + \frac{\pi }{6} + \frac{\pi }{3}t - \frac{\pi }{3}}}{2}} \right).\cos \left( {\frac{{\frac{\pi }{3}t + \frac{\pi }{6} - \frac{\pi }{3}t + \frac{\pi }{3}}}{2}} \right)} \right] = 2\left[2. {\cos \left( {\frac{\pi }{3}t - \frac{\pi }{{12}}} \right).\cos \frac{\pi }{4}} \right] = 2\sqrt 2 \cos \left( {\frac{\pi }{3}t - \frac{\pi }{{12}}} \right)\)
Vậy biên độ là \(2\sqrt 2 \), pha ban đầu \( - \frac{\pi }{{12}}\)

Ta có
\(\begin{array}{l}t = 0 \Rightarrow \omega t = 0\\t = \frac{T}{4} \Rightarrow \omega t = \omega .\frac{{\frac{{2\pi }}{\omega }}}{4} = \frac{\pi }{2}\\t = \frac{T}{2} \Rightarrow \omega t = \omega .\frac{{\frac{{2\pi }}{\omega }}}{2} = \pi \\t = \frac{{3T}}{4} \Rightarrow \omega t = \omega .\frac{{3.\frac{{2\pi }}{\omega }}}{4} = \frac{{3\pi }}{2}\\t = T \Rightarrow \omega t = \omega .\frac{{2\pi }}{\omega } = 2\pi \end{array}\)
a) \(A = 3cm,\varphi = 0\)
+) Với t=0 thì \(x = 3\cos \left( {\omega .0 + 0} \right) = 3\)
+) Với \(t = \frac{T}{4}\)thì \(x = 3\cos \left( {\frac{\pi }{2} + 0} \right) = 0\)
+) Với \(t = \frac{T}{2}\)thì \(x = 3\cos \left( {\pi + 0} \right) = - 3\)
+)Với \(t = \frac{{3T}}{4}\)thì \(x = 3\cos \left( {\frac{{3\pi }}{2} + 0} \right) = 0\)
+Với \(t = T\)thì \(x = 3\cos \left( {2\pi + 0} \right) = 3\)
b) \(A = 3cm,\varphi = - \frac{\pi }{2}\)
+) Với t=0 thì \(x = 3\cos \left( {0 - \frac{\pi }{2}} \right) = 0\)
+) Với \(t = \frac{T}{4}\)thì \(x = 3\cos \left( {\frac{\pi }{2} - \frac{\pi }{2}} \right) = 3\)
+) Với \(t = \frac{T}{2}\)thì \(x = 3\cos \left( {\pi - \frac{\pi }{2}} \right) = 0\)
+)Với \(t = \frac{{3T}}{4}\)thì \(x = 3\cos \left( {\frac{{3\pi }}{2} - \frac{\pi }{2}} \right) = 3\)
+Với \(t = T\)thì \(x = 3\cos \left( {2\pi - \frac{\pi }{2}} \right) = 0\)
c) \(A = 3cm,\varphi = \frac{\pi }{2}\)
+) Với t=0 thì \(x = 3\cos \left( {0 + \frac{\pi }{2}} \right) = 0\)
+) Với \(t = \frac{T}{4}\)thì \(x = 3\cos \left( {\frac{\pi }{2} + \frac{\pi }{2}} \right) = 3\)
+) Với \(t = \frac{T}{2}\)thì \(x = 3\cos \left( {\pi + \frac{\pi }{2}} \right) = 0\)
+)Với \(t = \frac{{3T}}{4}\)thì \(x = 3\cos \left( {\frac{{3\pi }}{2} + \frac{\pi }{2}} \right) = 3\)
+Với \(t = T\)thì \(x = 3\cos \left( {2\pi + \frac{\pi }{2}} \right) = 0\)

Vật đi qua vị trí cân bằng thì x = 0
Khi đó
\(\begin{array}{l}2\cos \left( {5t - \frac{\pi }{6}} \right) = 0\\ \Leftrightarrow \cos \left( {5t - \frac{\pi }{6}} \right) = 0\\ \Leftrightarrow 5t - \frac{\pi }{6} = \frac{\pi }{2} + k\pi \\\Leftrightarrow t = \frac{2\pi }{15} + \frac{{k\pi }}{5} ;k \in Z\end{array}\)
Do khoảng thời gian từ 0 đến 6 giây nên \(t \in \left[ {0;6} \right]\)
\(\begin{array}{l}0 \le \ \frac{{2\pi }}{{15}} + \frac{{k\pi }}{5} \le \ 6;k \in Z\\ \Rightarrow \frac{-2 }{3}\le \ k \le \ \frac{90 - 2\pi}{3\pi};k \in Z\end{array}\)
Do \(k \in Z\) nên \(k \in \left\{ {0;1;2;3;4;5;6;7;8} \right\}\)
Vậy trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng 9 lần.

\(sin\left(2t+\dfrac{\pi}{4}\right)\le1\Rightarrow x\le3\)
\(x_{max}=3\) khi \(sin\left(2t+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow2t+\dfrac{\pi}{4}=\dfrac{\pi}{2}+k2\pi\)
\(\Rightarrow t=\dfrac{\pi}{8}+k\pi\) với \(k\in Z\)

Vận tốc tức thời của dao động: \(f'\left( x \right) = - \sin x\)
Vận tốc tức thời của vật tại thời điểm \({x_0} = 2\left( s \right)\):\(f'\left( 2 \right) = - \sin \left( 2 \right) = 0,91\left( {m/s} \right)\)

\(v\left(t\right)=s'\left(t\right)=4\left[cos\left(2\pi t-\dfrac{\pi}{8}\right)\right]'\\ =-4\left(2\pi t-\dfrac{\pi}{8}\right)'sin\left(2\pi t-\dfrac{\pi}{8}\right)\\ =-8\pi sin\left(2\pi t-\dfrac{\pi}{8}\right)\)
Vận tốc của vật khi t = 5s là \(v\left(5\right)=-8\pi sin\left(10\pi-\dfrac{\pi}{8}\right)\approx9,6\left(m/s\right)\)

a) Vận tốc tức thời của con lắc: \(v(t) = - 4\pi \sin \left( {\pi t - \frac{{2\pi }}{3}} \right)\)
Gia tốc tức thời của con lắc: \(a(t) = - 4{\pi ^2}\cos \left( {\pi t - \frac{{2\pi }}{3}} \right)\)
b) Tại vận tốc tức thời của con lắc bằng 0, ta có:
\( - 4\pi \sin \left( {\pi t - \frac{{2\pi }}{3}} \right) = 0 \Leftrightarrow \sin \left( {\pi t - \frac{{2\pi }}{3}} \right) = 0 \Leftrightarrow \pi t - \frac{{2\pi }}{3} = 0 \Leftrightarrow t = \frac{2}{3}\)
Với \(t = \frac{2}{3} \Rightarrow a(t) = - \,4{\pi ^2}\cos \left( {\pi .\frac{2}{3} - \frac{2}{3}\pi } \right) = - \,4{\pi ^2}\)

\(v\left(t\right)=s'\left(t\right)=0,8\pi cos\left(0,8\pi t+\dfrac{\pi}{3}\right)\\ a\left(t\right)=v'\left(t\right)=-0,64\pi^2sin\left(0,8\pi t+\dfrac{\pi}{3}\right)\)
Vì:
\(v\left(t\right)=0\\ \Leftrightarrow0,8\pi cos\left(0,8\pi t+\dfrac{\pi}{3}\right)=0\\ \Leftrightarrow0,8\pi t+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k2\pi,k\in Z\\ \Leftrightarrow0,8\pi t=\dfrac{\pi}{6}+k\pi\\ \Leftrightarrow t=\dfrac{5}{24}+\dfrac{5k}{4}\)
Thời điểm vận tốc bằng 0, giá trị tuyệt đối của vật là
\(\left|a\left(\dfrac{5}{25}+\dfrac{5k}{4}\right)\right|=\left|-0,64\pi^2sin\left[0,8\pi\left(\dfrac{5}{24}+\dfrac{5k}{4}\right)+\dfrac{\pi}{3}\right]\right|\\ =0,64\pi^2\left|sin\left(\dfrac{\pi}{2}+k\pi\right)\right|\\ =0,64\pi^2\approx6,32\)
\(\Rightarrow\) Chọn C.

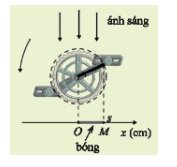
Độ dài bóng OM bằng 10 cm khi s = 10 hoặc s = -10.
Khi s = 10. Ta có: \(17cos5\pi t = 10 \Leftrightarrow cos5\pi t = \frac{{10}}{{17}}\)
Khi s = 10. Ta có: \(17cos5\pi t = - 10 \Leftrightarrow cos5\pi t = \frac{{ - 10}}{{17}}\)
Từ đó, ta có thể xác định được các thời điểm t bằng cách giải phương trình côsin.
a) Biên độ dao động \(A = - 5\); Pha ban đầu của dao động: \(\varphi = 0\)
b) Pha dao động tại thời điểm \(t = 2\) à \(\omega t + \varphi = 4\pi .2 = 8\pi \)
Chu kỳ \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = 0,2\)
Trong khoảng thời gian 2 giây, số dao động toàn phần vật thực hiện được là: \(\frac{2}{{0,2}} = 10\) (dao động)