Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phép đối xứng trục Oy có: x ' = − x y ' = y
Suy ra x = − x ' = − 2 y = y ' = 3
Vậy ảnh của điểm (2; 3) qua phép đối xứng trục Oy là D(-2; 3).
Đáp án D

Gọi d' là đường thẳng qua M và vuông góc d
\(\Rightarrow\) Phương trình d' có dạng:
\(1\left(x-2\right)-1\left(y-3\right)=0\Leftrightarrow x-y+1=0\)
Gọi N là giao điểm của d và d' thì tọa độ N thỏa: \(\left\{{}\begin{matrix}x+y=0\\x-y+1=0\end{matrix}\right.\) \(\Rightarrow N\left(-\frac{1}{2};\frac{1}{2}\right)\)
M' là ảnh của M qua phép đối xứng trục d \(\Rightarrow\) N là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_N-x_M=-3\\y_{M'}=2y_N-y_M=-2\end{matrix}\right.\) \(\Rightarrow M'\left(-3;-2\right)\)

+ Chứng minh hoàn toàn tương tự ta được
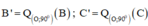
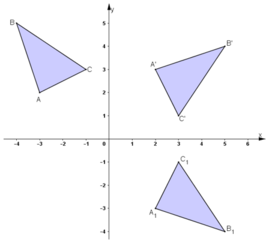
b. ΔA1B1C1 là ảnh của ΔABC qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc –90º và phép đối xứng qua trục Ox.
⇒ ΔA1B1C1 là ảnh của ΔA’B’C’ qua phép đối xứng trục Ox.
⇒ A1 = ĐOx(A’) ⇒ A1(2; -3)
B1 = ĐOx(B’) ⇒ B1(5; -4)
C1 = ĐOx(C’) ⇒ C1(3; -1).
a) + Ta có:
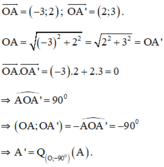
Đáp án A
Đường thẳng đi qua M và vuông góc với đường thẳng x + y = 0 có vectơ pháp tuyến n → ( 1 ; − 1 )
Phương trình đường thẳng Δ : ( x + 2 ) − ( y − 3 ) = 0 ⇒ x − y + 5 = 0
d ∩ Δ = I − 5 2 ; 5 2
⇒ M ' ( − 3 ; 2 )