Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (đồng) là giá tiền một quả quýt và y (đồng) là giá tiền một quả cam. Điều kiện
x > 0, y > 0 ta có hệ phương trình:
<=> <=>
<=> .
Trả lời: Giá tiền một quả quýt: 800 đồng, một quả cam 1400 đồng
Chúc bạn học tốt!

- Gọi x(nghìn đồng)là giá bán của mỗi quả dừa (0<x<25),y(nghìn đồng)là giá bán của mỗi quả thanh long (0<y<25)
- Vì bạn Hà mua một quả dừa vảo một quả thanh long hết 25 nghìn đồng, nên ta có pt:x+y=25
- Giá bán của 5 quả dừa là:5x(nghìn đồng),giá bán của 4 quả thanh long là:4y(nghìn đồng)
- Vì Bạn dũng mua 5 quả dừa và 4 quả thanh long hết 120 nghìn đồng,nên ta có pt:5x+4y=120
- giải hệ pt ra y=5(TMĐK),x=20(TMĐK)


Gọi số cam là x, số quýt là y (x, y ∈ N* ; x < 17, y < 17).
Quýt, cam 17 quả tươi ⇒ x + y = 17.
Mỗi quả quýt chia ba ⇒ Có 3y miếng quýt
Chia mười mỗi quả cam ⇒ Có 10x miếng cam
Tổng số miếng tròn 100 ⇒ 10x + 3y = 100.
Ta có hệ phương trình:
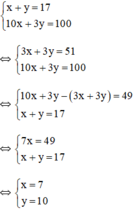
Vậy có 7 quả cam và 10 quả quýt.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình:
Bước 1: Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2: Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3: Đối chiếu nghiệm với điều kiện và kết luận.

Gọi số cam là x, số quýt là y (x, y ∈ N* ; x < 17, y < 17).
Quýt, cam 17 quả tươi ⇒ x + y = 17.
Mỗi quả quýt chia ba ⇒ Có 3y miếng quýt
Chia mười mỗi quả cam ⇒ Có 10x miếng cam
Tổng số miếng tròn 100 ⇒ 10x + 3y = 100.
Ta có hệ phương trình:
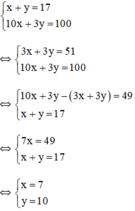
Vậy có 7 quả cam và 10 quả quýt.

Gọi số cam là x, số quýt là y. Điều kiện x, y là số nguyên dương.
Vậy có 7 quả cam và 10 quả quýt.
Gọi số quýt là x , số cam là y ( x ; y khác 0 )
Theo bài ra ta có :
\(x+y=17\)
\(\Rightarrow3\left(x+y\right)=51\left(1\right)\)
\(3x+10y=100\)
\(\Rightarrow3\left(x+y\right)+7y=100\left(2\right)\)
Lấy \(\left(2\right)-\left(1\right)\); ta được :
\(7y=100-51\)
\(\Rightarrow7y=49\)
\(\Rightarrow y=7\)
Mà \(x+y=17\)
\(\Rightarrow x=17-7=10\)
Vậy số quýt là 10 quả ; số cam là 7 quả

gọi giá 1 quả táo là a,,,số tiền mang là b,,,,
ta có hệ b/a-b/(a+2)=4 và b/(a-2)-b/a =6
cộng 2 pt rồi quy đồng tta đc 10(a^2-4)=4b
rút b theo a rồi thay vào 1 (.) 2 pt ở hệ,,,,,ra pt bậc 3

Gọi số cam là x ( quả )
số quýt là y (quả)
Điều kiện x, y > 0
Theo đề bài ta có hệ phương trình :
\(\left\{{}\begin{matrix}x+y=7\left(1\right)\\10x+3y=100\left(2\right)\end{matrix}\right.\)
(1) ⇔ y = 17 - x (3)
Thế (3) vào (2): 10x + 3(17 - x) = 100
⇔ 10x + 51 - 3x = 100 ⇔ 7x = 49 ⇔ x = 7
Từ đó y = 17 - 7 = 10
Vậy có 7 quả cam và 10 quả quýt.
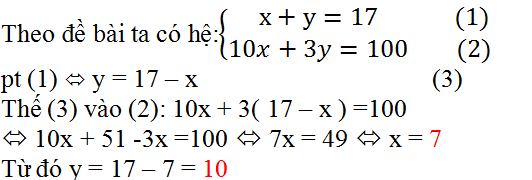
Gọi x là số lượng quả cam (x<45;x∈N*)
y là số lượng quả quýt (y<45;y∈N*)
Theo đề ta có hệ pt:
\(\left\{{}\begin{matrix}x+y=45\\4x+3y=165\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+3y=135\\4x+3y=165\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x=-30\\4x+3y=165\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=30\\4\cdot30+3y=165\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=30\\3y=45\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=30\left(tmđk\right)\\y=15\left(tmđk\right)\end{matrix}\right.\)
Vậy số lượng quả cam là 30 quả
số lượng quả quýt là 15 quả