Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong hoạt động trên, việc mua kem có thể có hai phương án một là mua kem que, hai là mua kem ốc quế. Đối với phương án mua kem que thì có tất cả 5 lựa chọn hay chính là 5 cách mua kem que. Phương án mua kem ốc quế thì có tất cả 4 lựa chon hay có 4 cách mua kem ốc quế. Số cách chọn mua một loại kem que hoặc kem ốc quế ở cửa hàng này là tổng số cách của hai phương án trên nên ta có tổng số cách là 5 + 4 = 9 cách.
Vậy có tất cả 9 cách để mua một loại kem que hoặc kem ốc quế ở cửa hàng này.
Trong hoạt động trên, việc mua kem có thể có hai phương án một là mua kem que, hai là mua kem ốc quế. Đối với phương án mua kem que thì có tất cả 5 lựa chọn hay chính là 5 cách mua kem que. Phương án mua kem ốc quế thì có tất cả 4 lựa chon hay có 4 cách mua kem ốc quế. Số cách chọn mua một loại kem que hoặc kem ốc quế ở cửa hàng này là tổng số cách của hai phương án trên nên ta có tổng số cách là 5 + 4 = 9 cách.
Vậy có tất cả 9 cách để mua một loại kem que hoặc kem ốc quế ở cửa hàng này.

Theo mình không thể biết chính xác đơn hàng đó đặt bao nhiêu cốc mà chỉ ước chừng được.
TH đơn hàng đặt ít nhất mà vẫn thỏa mãn các loại trên. Có 9 loại kem khác nhau, 5 loại trà khác nhau, tổng cộng 14 món, cho 14 món này vào 14 cốc.
TH đơn hàng nhiều nhất. Mỗi 1 món kem có thể đặt được nhiều nhất vào 3 cốc tương ứng với 3 loại đã đề cập (không thể để 1 món vào nhiều cốc cùng loại theo đề). Tổng cổng có thể đặt 9 loại kem vào 9.3=27 cốc. Tương tự đối với kem cũng vậy. 1 loại kem có thể đặt tối đa vào 3 cốc. 5 loại kem có thể đặt tối đa vào 15 cốc.
Tổng cộng TH này bên mua hàng đặt nhiều nhất 27+15=42 cốc.

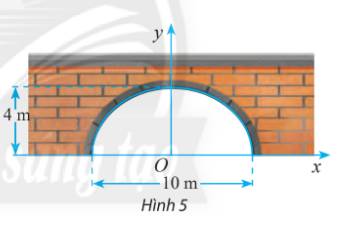
Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)

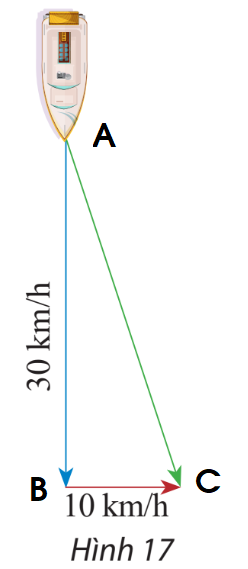
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).

a) Phương trình tham số của đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\)
b) Thay \(t = 2\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.2 = 81\\y = 1 + 30.2 = 61\end{array} \right.\)
Vậy khi \(t = 2\) thì tọa độ của ô tô là \(\left( {81;61} \right)\)
Thay \(t = 4\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.4 = 161\\y = 1 + 30.4 = 121\end{array} \right.\)
Vậy khi \(t = 4\) thì tọa độ của ô tô là \(\left( {161;121} \right)\)

Có 7 trận: Tứ kết 1, Tứ kết 2, Tứ kết 3, Tứ kết 4, Bán kết 1, Bán kết 2, Chung kết.

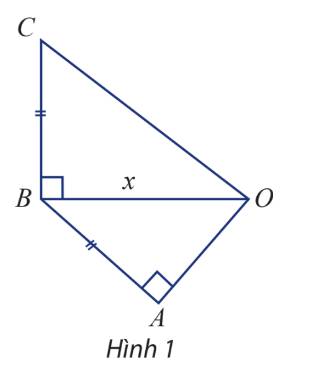
Gọi độ dài cạnh OB là x cm \(\left( {x > 0} \right)\)
Theo giả thiết ta có \(AB = BC = OB - 1 = x - 1\)
Áp dụng định lý pitago trong tam giác vuông OAB và OBC ta có:
\(OC = \sqrt {O{B^2} + B{C^2}} = \sqrt {{x^2} + {{\left( {x - 1} \right)}^2}} = \sqrt {2{x^2} - 2x + 1} \)
\(OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{x^2} - {{\left( {x - 1} \right)}^2}} = \sqrt {2x - 1} \)
a) \(OC = 3OA \Rightarrow \sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = 9\left( {2x - 1} \right)\\ \Rightarrow 2{x^2} - 20x + 10 = 0\end{array}\)
\( \Rightarrow \)\(x = 5 - 2\sqrt 5 \) và \(x = 5 + 2\sqrt 5 \)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \) ta thấy cả hai đều thỏa mãn phương trình
Vậy khi \(OB = 5 - 2\sqrt 5 \) hoặc \(OB = 5 + 2\sqrt 5 \)thì \(OC = 3OA\)
b) \(OC = \frac{5}{4}OB \Rightarrow \sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = \frac{{25}}{{16}}{x^2}\\ \Rightarrow \frac{7}{{16}}{x^2} - 2x + 1 = 0\end{array}\)\(\)
\( \Rightarrow x = \frac{4}{7}\) hoặc \(x = 4\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy khi \(OB = \frac{4}{7}\) hoặc \(OB = 4\) (cm) thì \(OC = \frac{5}{4}OB\)

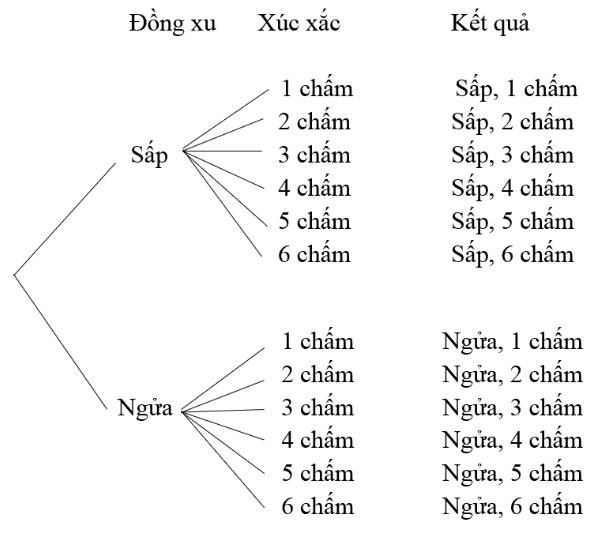
a) Kết quả của đồng xu và xúc xắc xảy ra đồng thời nên kết quả xảy ra gồm 2 kết quả liên tiếp nhau
Kết quả 1: Kết quả của đồng xu, có 2 kết quả: Sấp và ngửa
Kết quả 2: Kết quả của xúc xắc, có 6 kết quả: mỗi kết quả của mỗi mặt con xúc xắc
Áp dụng quy tắc nhân, ta có số kết quả có thẻ xuất hiện khi gieo đồng thời một đồng xu và một con xúc xắc là:
\(2.6 = 12\)
Vậy có 12 kết quả có thể xáy ra
b)

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)






+) Chọn một cái kem que: Có 5 cách (có thể chọn 1 trong 5 cái)
+) Chọn một cái kem ốc quế: Có 4 cách (có thể chọn 1 trong 4 cái)
Vậy tổng cả 9 cách chọn một trong 9 cái kem cả hai loại trong cửa hàng này.