Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=2\left(m-1\right)x+5-2m\)
\(\Leftrightarrow x^2-2\left(m-1\right)x-5+2m=0\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=2\left(m-1\right)\)
Ta có: \(x_1+x_2=6\)
\(\Leftrightarrow2\left(m-1\right)=6\)
\(\Leftrightarrow m-1=3\)
hay m=4
Vậy: m=4

a) Thay tọa dộ của điểm T vào dg thẳng d ta dc: -2.(-2) - 6 = -2 (Thỏa mãn)
Vậy điểm T có thuộc dg thẳng d
b) Pt hoành độ giao điểm của (d) và (P) là: -8x2 = -2x - 6
<=> 8x2 - 2x - 6 = 0
<=> (x - 1)(8x + 6) = 0 <=> \(\orbr{\begin{cases}x=1\\x=-\frac{3}{4}\end{cases}}\)
* Với x = 1 => y = -8
* Với x = -3/4 => y = -9/2
Tự kết luận nha

a: 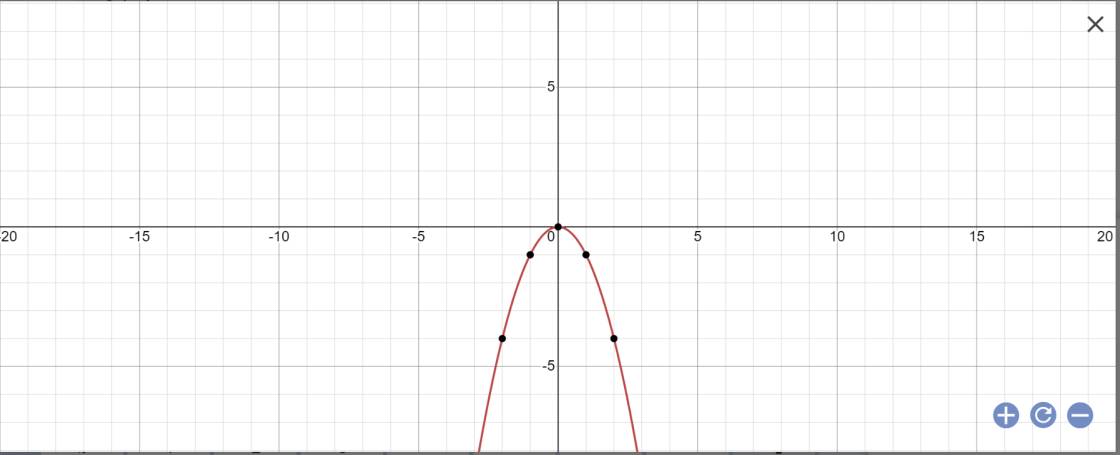
b: Phương trình OA có dạng là y=ax+b
Theo đề, ta có hệ:
0a+b=0 và a+b=1
=>b=0 và a=1
=>y=x
Vì (d)//OA nên (d): y=x+b
Thay x=2 và y=0 vào (d), ta được:
b+2=0
=>b=-2
=>y=x-2
PTHĐGĐ là:
-x^2-x+2=0
vì a*c<0
nên (P) luôn cắt (d) tại hai điểm phân biệt

Theo Cô si 4x+\frac{1}{4x}\ge24x+4x1≥2 , đẳng thức xảy ra khi và chỉ khi 4x=\frac{1}{4x}=1\Leftrightarrow x=\frac{1}{4}4x=4x1=1⇔x=41). Do đó
A\ge2-\frac{4\sqrt{x}+3}{x+1}+2016A≥2−x+14x+3+2016
A\ge4-\frac{4\sqrt{x}+3}{x+1}+2014A≥4−x+14x+3+2014
A\ge\frac{4x-4\sqrt{x}+1}{x+1}+2014=\frac{\left(2\sqrt{x}-1\right)^2}{x+1}+2014\ge2014A≥x+14x−4x+1+2014=x+1(2x−1)2+2014≥2014
Hơn nữa A=2014A=2014 khi và chỉ khi \left\{{}\begin{matrix}x=\dfrac{1}{4}\\2\sqrt{x}-1=0\end{matrix}\right.{x=412x−1=0 \Leftrightarrow x=\dfrac{1}{4}⇔x=41 .
Vậy GTNN = 2014

b) Để (d) đi qua (0;-1) thì
Thay x=0 và y=-1 vào y=ax+b, ta được:
\(a\cdot0+b=-1\)
\(\Leftrightarrow b=-1\)
Vậy: (d): y=ax-1
Phương trình hoành độ giao điểm của (P) và (d) là:
\(\dfrac{1}{2}x^2=ax-1\)
\(\Leftrightarrow\dfrac{1}{2}x^2-ax+1=0\)
\(\Delta=a^2-4\cdot\dfrac{1}{2}\cdot1=a^2-2\)
Để (d) và (P) tiếp xúc với nhau thì \(\Delta=0\)
\(\Leftrightarrow a^2=2\)
hay \(a\in\left\{\sqrt{2};-\sqrt{2}\right\}\)
Vậy: Để (d) tiếp xúc với (P) và (d) đi qua (0;-1) thì \(\left(a,b\right)=\left\{\left(\sqrt{2};-1\right);\left(-\sqrt{2};-1\right)\right\}\)