Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dễ thấy d // d’, ta có d ∩ Oy = A(0; 1); d’ ∩ Oy = A’(0; -4). Phép đối xứng tâm I biến Oy thành Oy thì I thuộc trục Oy; biến d thành d’ thì I là trung điểm của AA’ ⇒ I(0; -3/2).
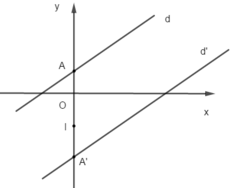
Đáp án D

Dễ thấy d và d' không song song với nhau.
Do đó trục đối xứng Δ của phép đối xứng biến d thành d' chính là đường phân giác của góc tạo bởi d và d'.
Từ đó suy ra Δ có phương trình:
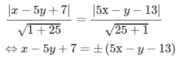
Từ đó tìm được hai phép đối xứng qua các trục:
Δ 1 có phương trình: x + y – 5 = 0,
Δ 2 có phương trình: x – y – 1 = 0.

Giao của d và d' với lần lượt là A(−2; 0) và A′(8;0). Phép đối xứng qua tâm cần tìm biến A thành A' nên tâm đối xứng của nó là I = (3;0).

Gọi giao điểm của d và l là điểm I. Tọa độ điểm I là nghiệm hệ:
x − 2 y + 2 = 0 x − y + 1 = 0 ⇔ x = 0 y = 1 ⇒ I ( 0 ; 1 )
Lấy A(4; 3) thuộc d. Phương trình đường thẳng a qua A và vuông góc với đường thẳng l có vecto chỉ phương là: u a → = n l → = ( 1 ; − 1 ) nên có vecto pháp tuyến là: n a → = ( 1 ; 1 )
Phương trình đường thẳng a: 1( x – 4) + 1.(y – 3) =0 hay x + y – 7 = 0
Gọi H là giao điểm của a và l.Tọa độ H là nghiệm hệ:
x − y + 1 = 0 x + y − 7 = 0 ⇔ x = 3 y = 4 ⇒ H ( 3 ; 4 )
Gọi A’ là điểm đối xứng với A qua H. Khi đó, H là trung điểm của AA’.
Suy ra: x A ' = 2 x H − x A y A ' = 2 y H − y A ⇔ x A ' = 2 y A ' = 5 ⇒ A ' ( 2 ; 5 )
Phương trình đường thẳng IA’: đi qua I(0; 1) và có vecto chỉ phương I A ' → ( 2 ; 4 ) ⇒ n → ( 2 ; − 1 ) . Phương trình IA’:
2( x- 0) - 1(y – 1) = 0 hay 2x – y + 1 = 0 chính là phương trình đường thẳng d’ đối xứng với d qua l.
Đáp án B

Phương trình đường thẳng d: x - y - 1= 0
Lấy M(x; y) thuộc d
Phép vị tự tâm O(0; 0) tỉ số k = 3 biến điểm M thành M’(x’; y’) thì O M ' → = 3 O M → ⇔ x ' = 3 x y ' = 3 y ⇔ x = 1 3 x ' y = 1 3 y '
Phép đối xứng trục Ox biến M’(x’; y’) thành M’’(x’’; y’’)
Thay vào phương trình d ta được: ⇔ x ' ' = x ' y ' ' = − y ' ⇔ x = 1 3 x ' ' y = − 1 3 y ' '
Hay x’’ + y’’ - 3 = 0
Vậy phương trình đường thẳng d’: x + y - 3 = 0.
Đáp án B

a) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua O.
Dùng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có :
M′ = (2; −3), phương trình của d′: 3x – y – 9 = 0, phương trình của đường tròn (C′): x 2 + y 2 − 2 x + 6 y + 6 = 0 .
b) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua I .
Vì I là trung điểm của MM' nên M′ = (4;1)
Vì d' song song với d nên d' có phương trình 3x – y + C = 0.
Lấy một điểm trên d, chẳng hạn N(0; 9).
Khi đó ảnh của N qua phép đối xứng qua tâm I là N′(2; −5).
Vì N' thuộc d nên ta có 3.2 − (−5) + C = 0. Từ đó suy ra C = -11.
Vậy phương trình của d' là 3x – y – 11 = 0.
Để tìm (C'), trước hết ta để ý rằng (C) là đường tròn tâm J(−1; 3),
bán kính bằng 2. Ảnh của J qua phép đối xứng qua tâm I là J′(3; 1).
Do đó (C') là đường tròn tâm J' bán kính bằng 2. Phương trình của (C') là x − 3 2 + y − 1 2 = 4 .



\(\left(d\right):2x-y-9=0\Leftrightarrow y=2x-9\)
\(\left(\Delta\right):x-3y+2=0\Leftrightarrow y=\frac{x+2}{3}\)
Phương trình hoành độ giao điểm của \(\left(d\right)\)và \(\left(\Delta\right)\)là:
\(2x-9=\frac{x+2}{3}\Leftrightarrow x=\frac{29}{5}\)
suy ra \(y=\frac{x+2}{3}=\frac{13}{5}\)
Do đó \(M\left(\frac{29}{5},\frac{13}{5}\right)\)là giao điểm của \(\left(d\right)\)và \(\left(\Delta\right)\).
Lấy \(N\left(0,-9\right)\in\left(d\right)\).
Lấy đường thẳng qua \(N\)và vuông góc với \(\Delta\), phương trình đường thằng đó có dạng: \(3x+y+c=0\)\(\left(\Delta'\right)\)
suy ra \(3.0-9+c=0\Leftrightarrow c=9\)
Giao điểm của \(\left(\Delta'\right)\)và \(\left(\Delta\right)\)là: \(I\left(\frac{-29}{10},-\frac{3}{10}\right)\)
\(N'\)là ảnh của \(N\)qua phép đối xứng qua trục \(\left(\Delta\right)\).
Khi đó \(I\)là trung điểm của \(NN'\).
Suy ra \(N'\left(-\frac{29}{5},\frac{42}{5}\right)\).
\(\left(d'\right)\)là đường thẳng đi qua \(M,N'\).
do đó có phương trình là: \(y=\frac{-1}{2}x+\frac{11}{2}\Leftrightarrow x+2y-11=0\).