Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do C thuộc Ox nên tọa độ có dạng: \(C\left(x;0\right)\)
Do trọng tâm G thuộc Oy \(\Rightarrow x_G=0\)
Mà \(x_A+x_B+x_C=3x_G\)
\(\Rightarrow1+\left(-3\right)+x=3.0\)
\(\Rightarrow x=2\)
\(\Rightarrow C\left(2;0\right)\)

a: vecto AB=(-3;-4)
vecto AC=(3;-2)
Vì -3/3<>-4/2-2
nên A,B,C là ba đỉnh của 1 tam giác
b: Tọa độ G là:
x=(2-1+5)/3=2 và y=(3-1+1)/3=2
=>G(2;2) và A(2;3)
Tọa độ I là:
x=(2+2)/2=2 và y=(2+3)/2=2,5
c: K thuộc Oy nên K(0;y)
vecto AI=(0;-0,5); vecto AK=(-2;y-3)
Theo đề, ta có:
0/-2=-0,5/y-3
=>-0,5/y-3=0
=>Ko có K thỏa mãn

Tọa độ trọng tâm G của tam gác MNP là:
x G = x M + x N + x P 3 = 0 + ( − 3 ) + 9 3 = 2 y G = y M + y N + y P 3 = 4 + 2 + ( − 3 ) 3 = 1 ⇒ G ( 2 ; 1 )
Đáp án D

a)
Ta có: \(\overrightarrow {AB} = \left( {2 - 1;4 - 3} \right) = \left( {1;1} \right),\;\overrightarrow {AC} = \left( { - 3 - 1;2 - 3} \right) = \left( { - 4; - 1} \right)\)
Hai vectơ này không cùng phương (vì \(\frac{1}{{ - 4}} \ne \frac{1}{{ - 1}}\)).
Do đó các điểm A, B, C không cùng nằm trên một đường thẳng.
Vậy A, B, C là ba đỉnh của một tam giác.
b) Trung điểm M của đoạn thẳng AB có tọa độ là \(\left( {\frac{{1 + 2}}{2};\frac{{3 + 4}}{2}} \right) = \left( {\frac{3}{2};\frac{7}{2}} \right)\)
c) Trọng tâm G của tam giác ABC có tọa độ là \(\left( {\frac{{1 + 2 + \left( { - 3} \right)}}{3};\frac{{3 + 4 + 2}}{3}} \right) = \left( {0;3} \right)\)
d) Để O(0; 0) là trọng tâm của tam giác ABD thì \(\left( {0;0} \right) = \left( {\frac{{{x_A} + {x_B} + {x_D}}}{3};\frac{{{y_A} + {y_B} + {y_D}}}{3}} \right)\)
\( \Leftrightarrow \left( {0;0} \right) = \left( {\frac{{1 + 2 + x}}{3};\frac{{3 + 4 + y}}{3}} \right)\)
\(\begin{array}{l} \Leftrightarrow \left( {0;0} \right) = \left( {1 + 2 + x;3 + 4 + y} \right)\\ \Leftrightarrow \left( {0;0} \right) = \left( {x + 3;y + 7} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}0 = x + 3\\0 = y + 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = - 7\end{array} \right.\end{array}\)
Vậy tọa độ điểm D là (-3; -7).

1.
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=-\dfrac{3}{2}\\y_I=\dfrac{y_A+y_B}{2}=1\end{matrix}\right.\) \(\Rightarrow I\left(-\dfrac{3}{2};1\right)\)
\(\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}=0\\y_G=\dfrac{y_A+y_B+y_C}{3}=0\end{matrix}\right.\) \(\Rightarrow G\left(0;0\right)\)
2.
\(\left\{{}\begin{matrix}\overrightarrow{CI}=\left(-\dfrac{9}{2};3\right)\\\overrightarrow{AG}=\left(-2;-3\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}CI=\sqrt{\left(-\dfrac{9}{2}\right)^2+3^2}=\dfrac{3\sqrt{13}}{2}\\AG=\sqrt{\left(-2\right)^2+\left(-3\right)^2}=\sqrt{13}\end{matrix}\right.\)
3.
Gọi \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-7;-4\right)\\\overrightarrow{DC}=\left(3-x;-2-y\right)\end{matrix}\right.\)
\(ABCD\) là hbh \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow\left\{{}\begin{matrix}-7=3-x\\-4=-2-y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=10\\y=2\end{matrix}\right.\)
\(\Rightarrow D\left(10;2\right)\)
4. Gọi \(H\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{CH}=\left(x-3;y+2\right)\\\overrightarrow{AH}=\left(x-2;y-3\right)\\\overrightarrow{BC}=\left(8;-1\right)\end{matrix}\right.\)
H là trực tâm \(\Leftrightarrow\left\{{}\begin{matrix}AH\perp BC\\CH\perp AB\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{CH}.\overrightarrow{AB}=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8\left(x-2\right)-1\left(y-3\right)=0\\-7\left(x-3\right)-4\left(y+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8x-y=13\\-7x-4y=-13\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{5}{3};\dfrac{1}{3}\right)\)
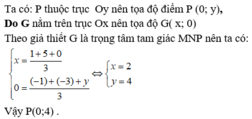

Đề thiếu. Bạn coi lại đề.