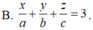Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp giải: Xác định tọa độ ba điểm A, B, C và gọi tâm I, sử dụng điều kiện cách đều IA=IB=IC=IO để tìm tọa độ tâm I của mặt cầu
Lời giải:
Gọi A(a;0;0), B(0;b;0), C(0;0;c) => Tọa độ trọng tâm G là
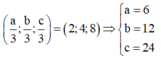
Gọi tâm mặt cầu (S) là I(x;y;z) => IO =IA = IB =IC
![]()
![]()
![]()
![]()
Vậy tọa độ tâm mặt cầu là I(3;6;12)

Đáp án B
Vì OA, OB, OC đôi một vuông góc và M là trực tâm tam giác ABC => OM ⊥ (ABC)
Suy ra mp(ABC) nhận O M → làm véc tơ pháp tuyến và đi qua điểm M(1;2;3)
Vậy phương trình mp(P):
![]()
<=> x +2y+3z -14=0

Đáp án D
Ta có: OA → OB, OC => OA → (OBC) => OA → BC
Mặt khác vì AM → BC (M là trực tâm tam giác ABC) nên ta suy ra BC → (OAM) => BC → OM
Chứng minh tương tự ta được AC → OM. Do đó OM → (ABC). Ta chọn: n p → = OM → = (1; -2; 3)
Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) - 2(y + 2) + 3(z - 3) = 0 ⇔ x - 2y + 3z - 14 = 0

Đáp án D
Ta có OA ⊥ OB, OC => OA ⊥ (OBC) => OA ⊥ BC.
Mặt khác ta có AM ⊥ BC nên ta suy ra BC ⊥ (OAM) => BC ⊥ OM
Chứng minh tương tự ta được AC ⊥ OM. Do đó OM ⊥ (ABC).
Ta chọn n P → = OM → = (1; 2; 2). Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x - 1) + 2(y - 2) + 2(z - 2) = 0 <=> x + 2y + 2z - 9 = 0
Chọn D

Chọn B.
![]() là giao điểm của mặt phẳng (α) các trục Ox, Oy, Oz
là giao điểm của mặt phẳng (α) các trục Ox, Oy, Oz
Phương trình mặt phẳng
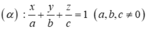
Ta có G là trọng tâm tam giác ABC
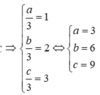
![]()
![]()

Chọn D
Vì A thuộc Ox nên A(a;0;0).
Vì B thuộc Oy nên B(0;b;0).
Vì C thuộc Oz nên C(0;0;c).
G là trọng tâm tam giác ABC khi và chỉ khi


Chọn B
Gọi A (a; 0; 0), B(0; b; 0) và C(0; 0; c) với abc ≠ 0. Phương trình mặt phẳng (P) đi qua ba điểm A, B, C là
![]() .
.
Vì M(1;2;3) ∈ (P) nên ta có: ![]() .
.
Điểm M là trực tâm của tam giác ABC.
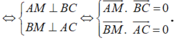

Phương trình mặt phẳng (P) là: ![]() <=> x + 3y + 2z - 14 = 0
<=> x + 3y + 2z - 14 = 0