

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



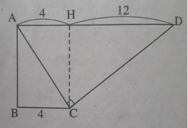
Kẻ đường cao CH của tam giác ACD vuông tại C. Khi đó
AH = BC = 4, HD = AD – AH = 12.
Từ đó
H C 2 = HA.HD = 48, vậy HC = 4 3
Trong tam giác vuông HCD, ta có
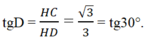
Nên ∠ D = 30 ° . Suy ra ∠(BCD) = 180 ° - 30 ° = 150 °

a. Kẻ BE ⊥ CD
Suy ra tứ giác ABED là hình chữ nhật
Ta có: AD = BE
AB = DE = 4 (cm)
Suy ra: CE = CD – DE = 9 – 4 = 5 (cm)
Áp dụng định lí Pitago vào tam giác vuông BCE ta có :
BC2 = BE2 + CE2
Suy ra : BE2 = BC2 – CE2 = 132 – 52 = 144
BE = 12 (cm)
Vậy: AD = 12 (cm)
b. Gọi I là trung điểm của BC
Ta có: IB = IC = (1/2).BC = (1/2).13 = 6,5 (cm) (1)
Kẻ IH ⊥ AD. Khi đó HI là đường trung bình của hình thang ABCD.
Từ (1) và (2) suy ra : IB = IH = R
Vậy đường tròn (I ; BC/2 ) tiếp xúc với đường thẳng AD

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

a . Gọi O là tâm của đường tròn có đường kính BC.
Xét \(\Delta\)BMC vuông tại M có O là trung điểm của BC (OB=OC)
\(\Rightarrow CB=MO=OC\)
\(\Leftrightarrow M\in\left(O;OB\right)\left(1\right)\)
Xét hình thang ABCD có :
M là trung điểm của AD;O là trung điểm của BC
\(\Rightarrow MO\) là đường trung bình
\(\Leftrightarrow\)AB//MO
Mà AD\(\perp\)AB
\(\Rightarrow MO\perp AD\left(2\right)\)
Từ \(\left(1\right)\left(2\right)suyra\) AD là tiếp tuyến của đường tròn đường kính BC