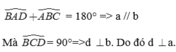
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
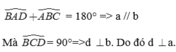
Ta có: \(\widehat{BAD}+\widehat{ABC}=110^o+70^o=180^o\)
Mà 2 góc này là 2 góc trong cùng phía ⇒a//b
a//b, b⊥d⇒a⊥d
Ta có \(\widehat{BAD}\) + \(\widehat{ABC}\) = 180° => a // b
Mà \(\widehat{BCD}\) = 90°=>d ⊥ b. Do đó d ⊥ a
Ta có B A D ^ + A B C ^ = 180° => a // b
Mà B C D ^ = 90°=>d ⊥ b. Do đó d ⊥ a
Trong trường hợp hình d) thì a và b không song song với nhau vì tổng hai góc trong cùng phía không bằng \(180^0\)
trong hình a) ta có : 180 - 36 =144 (vì 2 góc bù nhau )
vậy a song song b (vì 2 góc đồng vị bằng nhau)
trong hình b) ta có : a song song b (vì 2 so le ngoài bằng nhau )
trong hình c) ta có : 180 - 50 =130 (vì 2 góc bù nhau )
vậy a song song b (vì 2 góc đồng vị bằng nhau )
trong hình d) a không song song với b ( vì hai góc trong cùng phía không bù nhau )
a) Ta có PA = PB (A, B nằm trên cung tròn có tâm P) CA = CB (hai cung tròn AB có tâm A và B có bán kính bằng nhau; C la giao điểm của 2 cung)
Vậy P; C cách đều A và B nên đường thẳng CP là đường trung trực của AB nên
PC ⊥ d
b) Một cách vẽ khác
- Lấy điểm A bất kì trên d
- Vẽ cung tròn tâm A bán kính AP cắt đường thẳng d tại M
- Vẽ cung tròn tâm M bán kính MP cắt cung tròn tâm A tại C
- Vẽ đường thẳng PC, đường thẳng PC chính là đường vuông góc với d.
=> PC ⊥ d (đpcm)
Hướng dẫn:
a) Ta có PA = PB (A, B nằm trên cung tròn có tâm P) CA = CB (hai cung tròn AB có tâm A và B có bán kính bằng nhau; C la giao điểm của 2 cung)
Vậy P; C cách đều A và B nên đường thẳng CP là đường trung trực của AB nên
PC ⊥ d
b) Một cách vẽ khác
- Lấy điểm A bất kì trên d
- Vẽ cung tròn tâm A bán kính AP cắt đường thẳng d tại M
- Vẽ cung tròn tâm M bán kính MP cắt cung tròn tâm A tại C
- Vẽ đường thẳng PC, đường thẳng PC chính là đường vuông góc với d.
=> PC ⊥ d (đpcm)
vẽ luôn hình ấy ạ 
Tớ camon cái cậu làm giúp tớ lắm í ạ 
Caccau giúp tớ với nhé 
Những ai làm rồi hoặc biết làm chỉ tớ với 
