Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/
+ + A B + C q1 q2 q3 F F F 23 13 hl → → →
Ta có: \(\vec{F_{hl}}=\vec{F_{13}}+\vec{F_{23}}\)
Do \(\vec{F_{13}}\uparrow\downarrow\vec{F_{23}}\) nên: \(F_{hl}=\left|F_{13}-F_{23}\right|\) (1)
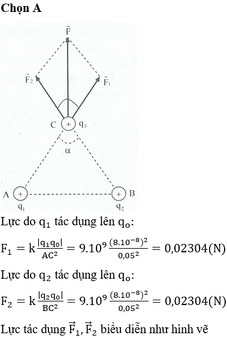
\(F_{13}=9.10^9\frac{\left|q_1q_2\right|}{AC^2}=0,045N\)
\(F_{23}=9.10^9\frac{\left|q_1q_2\right|}{BC^2}=0,01N\)
Thay vào (1) ta được \(F_{hl}=0,035N\)
b/
+ + + A B D q1 q2 q3 F F F 23 13 hl → → →
Hợp lực: \(\vec{F_{hl}}=\vec{F_{13}}+\vec{F_{23}}\)
Do hai lực cùng phương cùng chiều nên độ lớn:
\(F_{hl}=F_{13}+F_{23}\)(2)
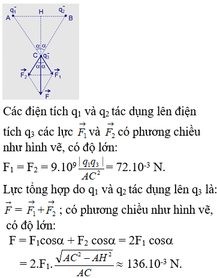
\(F_{13}=9.10^9.\frac{\left|q_1q_3\right|}{AD^2}=7,2.10^{-3}N\)
\(F_{23}=9.10^9.\frac{\left|q_2q_3\right|}{BD^2}=0,9.10^{-3}N\)
Thế vào (2) ta được \(F_{hl}=8,1.10^{-3}N\)

Đáp án A
Dùng phương pháp số phức tổng hợp lực (chọn trục nằm ngang làm trục chuẩn):
F → = F → A C + F → B C = F A C ∠ π 2 + F B C < 0
= 3 , 75 ∠ π 2 + 5 , 625 = 15 13 8 ∠ 0 , 588 N


a) thay số vào CT là ra thôi:\(F=\dfrac{kq_1q_2}{AB^2}\)
b) M nằm trên đường thẳng AB, ngoài AB và gần phía A. q1 sẽ đẩy q3, q2 sẽ hút q3
\(F_{13}=\dfrac{kq_1q_3}{MA^2}\)
\(F_{23}=\dfrac{kq_2q_3}{MB^2}\)
lực điện tác dụng lên q3:\(F_3=\left|F_{13}-F_{23}\right|=...\)
(vì một cái đẩy một cái hút nên phải trừ ra nha )