Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

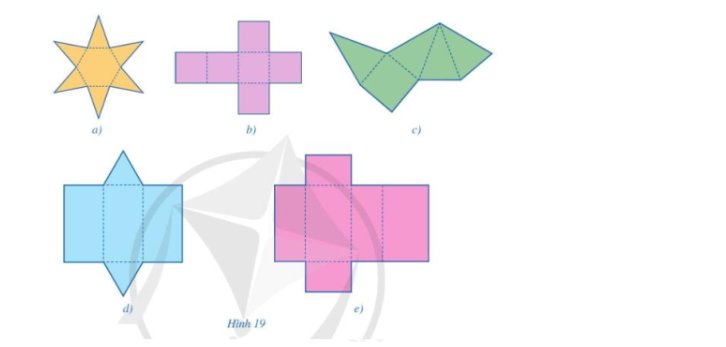
Miếng bìa hình 19c có thể gấp lại (theo các nét đứt) để được hình chóp tứ giác đều.

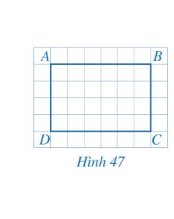
Tứ giác ABCD có: \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\)

Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

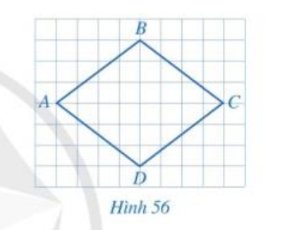
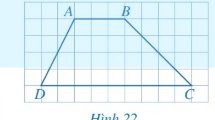
Hai cạnh AB và CD của tứ giác ABCD có song song với nhau.

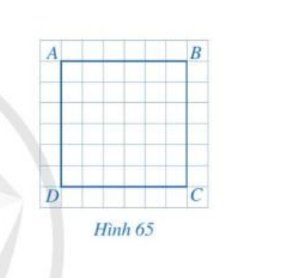
Do tứ giác ABCD là hình vuông nên các cạnh AB, BC, CD, DA bằng nhau và các góc \(\widehat{ABC},\widehat{BCD},\widehat{CDA},\widehat{DAB}\) bằng nhau và bằng 90o.

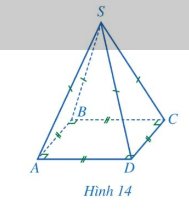
Hình chóp tứ giác đều S.ABCD có:
- Mặt đáy ABCD là hình vuông.
- Các mặt bên là SAB, SBC, SCD, SDA là những tam giác cân tại S.
- Các cạnh đáy AB, BC, CD, DA bằng nhau.
- Các cạnh bên SA, SB, SC, SD bằng nhau.
- S gọi là đỉnh của hình chóp đều S. ABCD

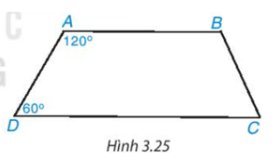
Do \(\widehat{A}+\widehat{D}=120^o+60^o=180^o\)
\(\Rightarrow AB//CD\)
\(\Rightarrow\) ABCD là hình thang.
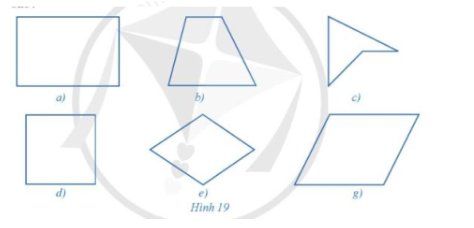

Tứ giác ở hình 19c không phải là tứ giác lồi vì: Tứ giác hình 19c nằm về 2 phía của diện tích chứa 1 cạnh bất kì.