Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
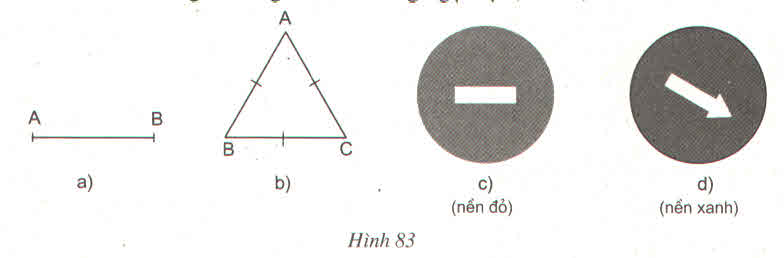
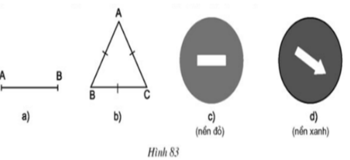
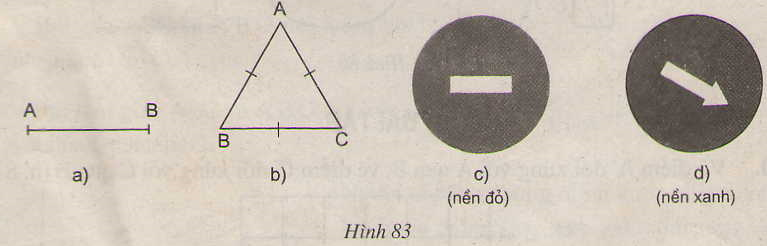
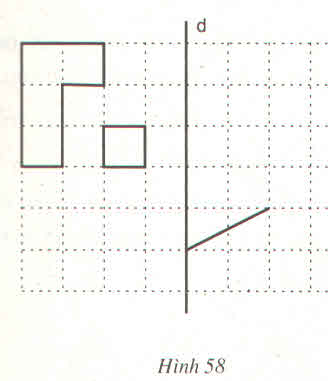
- Hình 83a có tâm đối xứng là trung điểm của đoạn thẳng AB
- Hình 83b không có tâm đối xứng
(Lưu ý: Trọng tâm đồng thời là trực tâm của tam giác đều ABC không phải tâm đối xứng của tam giác đó)
- Hình 83c có tâm đối xứng là tâm của hình tròn.
- Hình 83d không có tâm đối xứng.
Hình 83a, c có tâm đối xứng.
Hình 83a có tâm đối xứng là trung điểm của đoạn thẳng AB,
Hình 83c có tâm đối xứng là tâm của đường tròn.
Bài giải:
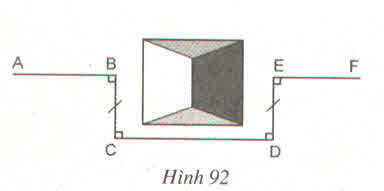
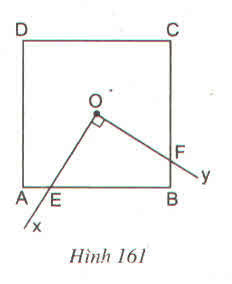
Tứ giác BCDE có:
BC // DE (vì cùng vuông góc với CD)
BC = DE
nên BCDE là hình chữ nhật
Do đó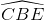 
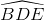= 900 , 
= 900
Suy ra AB và EF cùng nằm trên một đường thẳn
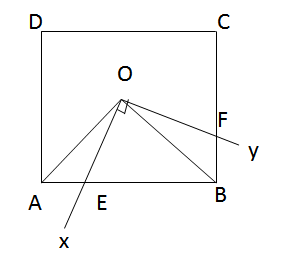
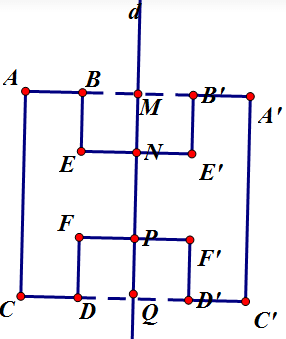
Nối OA, OB.
Xét \(\Delta\)AOE và \(\Delta\)BOF có:
+ \(\widehat{AOE}=\widehat{BOF}\) (cùng phụ với \(\widehat{BOE}\))
+ OA = OB (O là tâm đối xứng)
+ \(\widehat{OAE}=\widehat{OBE}=45^o\)
=> ∆AOE = ∆BOF (g - c - g)
Do đó: \(S_{OEBF}=S_{OEB}+S_{OBF}=S_{OEB}+S_{OAE}=S_{OAE}+S_{OEB}=S_{OAB}\)
Vậy \(S_{OEBF}=\dfrac{1}{4}S_{ABCD}\)
Nối OA, OB.
Xét ΔAOE và ΔBOF có:
+) \(\widehat{AOE}=\widehat{BOF}\) ( cùng phụ với BOE )
+) OA = OB ( O là tâm đối xứng )
+) \(\widehat{OAE}=\widehat{OBF}=45^0\)
⇒ ΔAOE = ΔBOF.
⇒ \(S_{OEBF}=S_{OEB}+S_{OBF}=S_{OEB}+S_{OAE}=S_{OAE}+S_{OAB}\)
⇒ \(S_{OEBF}=\frac{1}{4}S_{ABCD}.\)
Bài giải:
Hình 83a, c có tâm đối xứng.
Hình 83a có tâm đối xứng là trung điểm của đoạn thẳng AB,
Hình 83c có tâm đối xứng là tâm của đường tròn.