Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ OK ⊥ CD ⇒ CK = DK = (1/2).CD
Kẻ OH ⊥ AB ⇒ AH = BH = (1/2).AB
Vì AB // CD nên H, O, K thẳng hàng
Áp dụng định lí Pitago vào tam giác vuông OBH ta có:
O B 2 = B H 2 + O H 2
Suy ra: O H 2 = O B 2 - B H 2 = 25 2 - 20 2 = 225
OH = 15 (cm)
Áp dụng định lí Pitago vào tam giác vuông ODK ta có:
O D 2 = D K 2 + O K 2
Suy ra: O K 2 = O D 2 - D K 2 = 25 2 - 24 2 = 49
OK = 7 (cm)
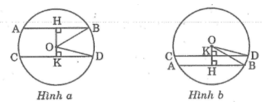
* Trường hợp O nằm giữa hai dây AB và CD (hình a):
HK = OH + OK = 15 + 7 = 22 (cm)
* Trường hợp O nằm ngoài hai dây AB và CD (hình b):
HK = OH – OK = 15 – 7 = 8 (cm)

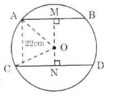
Kẻ OM ⊥ AB, ON ⊥ CD.
Ta thấy M, O, N thẳng hàng. Ta có:
![]()
Áp dụng định lí Pitago trong tam giác vuông AMO có:
OM2 = OA2 – AM2 = 252 – 202 = 225
=> OM = √225 = 15cm
=> ON = MN – OM = 22 – 15 = 7 (cm)
Áp dụng định lí Pitago trong tam giác vuông CON có:
CN2 = CO2 – ON2 = 252 – 72 = 576
=> CN = √576 = 24
=> CD = 2CN = 48cm

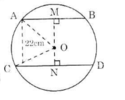
Kẻ OM ⊥ AB, ON ⊥ CD.
Ta thấy M, O, N thẳng hàng. Ta có:
![]()
Áp dụng định lí Pitago trong tam giác vuông AMO có:
O M 2 = O A 2 – A M 2 = 25 2 – 20 2 = 22 2
=> OM = √225 = 15cm
=> ON = MN – OM = 22 – 15 = 7 (cm)
Áp dụng định lí Pitago trong tam giác vuông CON có:
C N 2 = C O 2 – O N 2 = 25 2 – 7 2 = 576
=> CN = √576 = 24
=> CD = 2CN = 48cm

22cm A M B C N D O
Kẻ \(OM\perp AB , ON\perp CD\)
Ta thấy M, O, N thẳng hàng. Ta có:
\(AM=\frac{1}{2}AB=20cm ; MN=22cm\)
Áp dụng định lí Pitago trong tam giác vuông AMO có:
OM2 = OA2 – AM2 = 252 – 202 = 225
=> OM = \(\sqrt{225}\) = 15cm
=> ON = MN – OM = 22 – 15 = 7 (cm)
Áp dụng định lí Pitago trong tam giác vuông CON có:
CN2 = CO2 – ON2 = 252 – 72 = 576
=> CN = \(\sqrt{576}\) = 24
=> CD = 2CN = 48cm

Gọi H,K lần lượt là trung điểm của AB,CD
ΔAOB cân tại O
mà OH là đường trung tuyến
nên OH vuông góc AB
=>d(O;AB)=OH
ΔOCD cân tại O
mà OK là đường trung tuyến
nên OK vuông góc CD
=>d(O;CD)=OK
H là trung điểm của AB
=>HA=HB=40/2=20cm
K là trung điểm của CD
=>KC=KD=48/2=24cm
ΔOHA vuông tại H
=>OH^2+HA^2=OA^2
=>OH^2=25^2-20^2=225
=>OH=15(cm)
ΔOKC vuông tạiK
=>OK^2+KC^2=OC^2
=>OK=7(cm)
OH vuông góc AB
AB//CD
=>OH vuông góc CD
mà OK vuông góc CD
nên O,H,K thẳng hàng
=>HK=OH+OK=7+15=22cm
=>d(AB;CD)=22cm

*, Kẻ OH vuông AB, H \(\in\)AB
=> H là trung điểm AB
=> HB = AB/2 = 40/2 = 20 cm
Theo định lí Pytago tam giác OBH vuông tại H
\(OH=\sqrt{OB^2-HB^2}=15\)cm
*, Kẻ OT vuông CD, T \(\in\)CD
=> T là trung điểm CD
=> TD = DC/2 = 48/2 = 24 cm
Theo định lí Pytago tam giác ODC vuông tại T
\(OT=\sqrt{OD^2-DT^2}=7\)cm