Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các kết quả thuận lợi cho biến cố A là A = {Hương; Hồng; Dung}.
Các kết quả thuận lợi cho biến cố B là B = { Hương; Hồng; Hoàng}.

a) Công việc cần qua hai công đoạn
Công đoạn 1 cần chọn một bạn nữ từ 4 bạn có 4 cách
Công đoạn 2 cần chọn 2 bạn nam từ 5 bạn và không tính đến thứ tự có \(C_5^2\) cách
Vậy có \(4.C_5^2 = 40\)kết quả thuận lợi cho biến cố “Trong ba bạn được chọn có đúng một bạn nữ”
b) Ba bạn được chọn không có bạn nam nào tức là ba bạn đều là nữ, ta chọn ra 3 bạn nữ từ 4 bạn và không tính đến thứ tự có \(C_4^3 = 4\) cách
Vậy có 4 kết quả thuận lợi cho biến cố “Trong ba bạn được chọn không có bạn nam nào”

a: Số cách chọn là: \(C^3_{25}=2300\left(cách\right)\)
b: Số cách chọn là: \(C^1_{15}\cdot C^2_{24}=4140\left(cách\right)\)

Hai phương trình (cùng ẩn) được gọi là tương đương nếu chúng có cùng tập nghiệm.
Hai phương trình \(2x-5=0\)và \(3x-\dfrac{15}{2}=0\) tương đương với nhau vì cùng có nghiệm duy nhất \(x=\dfrac{5}{2}\)
Hai phương trình (cùng ẩn) được gọi là tương đương nếu chúng có cùng tập nghiệm.
Nếu f(x) = g(x) tương đương với f1(x) = g1(x) thì ta viết:
f(x) = g(x)  f1(x) = g1(x)
f1(x) = g1(x)
Ví dụ:
|
Hai phương trình 2x - 5 = 0 và
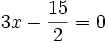 tương đương với nhau vì cùng có nghiệm duy nhất tương đương với nhau vì cùng có nghiệm duy nhất 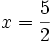 . . |
| |

- Hai phương trình có cùng tập nghiệm thì tương đương nhau.
- Ví dụ hai phương trình:
x2 - 3x + 2 = 0 và (x - 1)(x - 2)(x2 + x + 1) = 0
là hai phương trình tương đương vì chúng có cùng tập nghiệm là {1, 2}.

a) Số nguyên dương nhỏ hơn 100 luôn có 1 hoặc 2 chữ số nên ta có không gian mẫu của phép thử trên là: \(\Omega = \left\{ {1,2,3,4,5,...98,99} \right\}\)
b) Tập hợp biến cố A: “Số được chọn là số chính phương” là:
\(A = \left\{ {{a^2}\left| {a = 1,2,...,9} \right.} \right\}\)
c) Cứ 4 số thì có 1 số chia hết cho 4, số nhỏ nhất là 4 và lớn nhất là 96 nên số kết quả thuận lợi cho biến cố B là \(\dfrac{96-4}{4}+1=24\).
Vậy có 24 kết quả thuận lợi cho biến cố B: “Số được chọn chia hết cho 4”
\(a,\Omega=\left\{1;2;3;4;5;...;98;99\right\}\\ b,A=\left\{1;4;9;16;25;36;49;64;81\right\}\\c, B=\left\{4;8;16;20;24;...;92;96\right\}\\ Số.kết.quả.thuận.lợi.cho.B:\left(96-4\right):4+1=24\left(kết.quả\right)\)

a) Hai bạn được chọn ở HĐ2a có vai trò như nhau, nói cách khác là không quan trọng thứ tự chọn.
Còn ở HĐ2b thì hai bạn có có vai trò khác nhau, nói cách khác là có xếp thứ tự lần lượt là lớp trưởng và lớp phó.
b) Số cách chọn 2 bạn (có xếp thứ tự) là 12 cách chọn.
Nhưng ở HĐ2a thì hai bạn có vai trò như nhau nên ta chia kết quả cho 2, tức là có 6 cách chọn (khi không xếp thứ tự)

Tổng số khả năng có thể xảy ra của phép thử là \(n\left( \Omega \right) = C_{12}^4\)
a) Số kết quả thuận lợi cho biến cố “Bốn bạn thuộc 4 tổ khác nhau” là số cách sắp xếp 4 bạn vào 4 tổ có \(4!\) cách
Vậy xác suất của biến cố “Bốn bạn thuộc 4 tổ khác nhau” là \(P = \frac{{4!}}{{C_{12}^4}} = \frac{8}{{165}}\)
b) Gọi A là biến cố “Bốn bạn thuộc 2 tổ khác nhau”
A xảy ra với 2 trường hợp sau:
TH1: 3 bạn cùng thuộc 1 tổ và 1 bạn thuộc tổ khác có \(C_4^3.C_3^1.C_2^1 = 24\) cách
TH2: cứ 2 bạn cùng thuộc 1 tổ \(C_4^2.C_3^1.C_2^2.C_2^1 = 36\) cách
Suy ra, số kết quả thuận lợi cho biến cố A là \(n\left( A \right) = 24 + 36 = 60\)
Vậy xác suất của biến cố “Bốn bạn thuộc 2 tổ khác nhau” là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{60}}{{C_{12}^4}} = \frac{4}{{33}}\)

a: Sô cách chọn là: \(C^6_{40}\left(cách\right)\)
b: Số cách chọn là:
\(C^4_{25}\cdot C^2_{15}+C^5_{25}\cdot C^1_{15}=2125200\left(cách\right)\)
Ta thấy biến cố C xảy ra khi và chỉ khi biến cố A không xảy ra.