K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 5 2017
Ta có : AB=AC
=> \(\Delta ABC\) là tam giác vuông cân tại A ( vì tam giác có 2 cạnh bằng nhau )
=> \(\widehat{ABC}=A\widehat{CB}\) ( hai cạnh đáy của tam giác cân )
=> \(\widehat{ABC}=A\widehat{CB}=45^0\)
=> \(\widehat{CBD}=\widehat{A}+\widehat{BCA}=135^0\) ( góc ngoài của tam giác )
Ta lại có:
BD=BC
=> \(\Delta BCD\) cân tại B ( vì tam giác có 2 cạnh bằng nhau )
=> \(\widehat{BDC}=\widehat{BCD}\) ( hai cạnh đáy của tam giác cân )
=> \(\widehat{BDC}=\widehat{BCD}=\dfrac{\left(180^0-135^0\right)}{2}=\dfrac{45^0}{2}=22,5^0\)
Mà \(\widehat{ACD}=\widehat{BCA}+\widehat{BCD}\)
=> \(\widehat{ACD}=45^0+22,5^0=67,5^0\)
Vậy trong \(\Delta ACD\) có :
\(\left\{{}\begin{matrix}\widehat{A}=90^0\\\widehat{ADC}=22,5^0\\\widehat{ACD}=67,5^0\end{matrix}\right.\)
13 tháng 5 2017
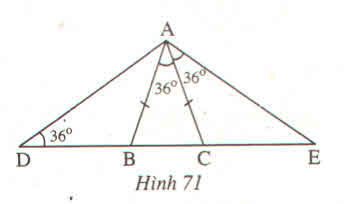
Tam giác ABC có AB = AC (theo đề bài)
Suy ra: tam giác ABC cân tại A( dựa theo định nghĩa tam giác cân)
=> góc ABC = góc ACB ( dựa theo tính chất tam giác cân)
=> góc ABC = góc ACB = \(\left(180^0-36^0\right):2=72^0\)
Có góc ACB + góc ACE = \(180^0\) (2 góc kề bù)
=> góc ACE = \(180^0\)- góc ACB
=> góc ACE = \(180^0-72^0=108^0\)
Tam giác ACE có góc CAE + góc CEA + góc ACE = \(180^0\)(tổng 3 góc của 1 tam giác)
=> góc CEA = \(180^0-\left(108^0+36^0\right)=36^0\)(*)
Tam giác ADE có góc BDA = góc CEA = \(36^0\)
=> tam giác ADE cân tại A ( dựa theo tính chất của tam giác cân)
SG
1
DN
20 tháng 4 2017
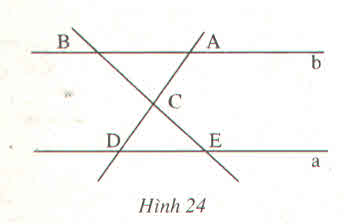
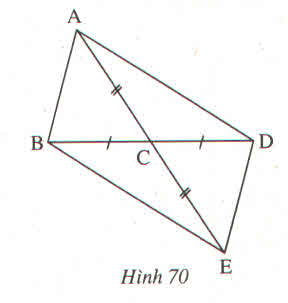
Ta có:
^ECD = ^ACB (2 góc đối đỉnh).
Vì a // b nên:
^ABC = ^CED và ^CDE = BAC (2 góc so le trong)
Vậy các cặp góc bằng nhau của 2 tam giác CAB và CDE là: ^ACB = ^ECD; ^BAC = ^CDE; ^ABC = ^CED.
Câu 1:
\(\left\{{}\begin{matrix}b-c=30\\b+c=110\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=70\\c=40\end{matrix}\right.\)
Vậy: ΔABC có hai góc bằng nhau