Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(\dfrac{{AG}}{{AM}} = \dfrac{6}{9} = \dfrac{2}{3}\);
\(\dfrac{{BG}}{{BN}} = \dfrac{4}{6} = \dfrac{2}{3}\);
\(\dfrac{{CG}}{{CP}} = \dfrac{4}{6} = \dfrac{2}{3}\).

Cho tam giác HPG có 3 trung tuyến HM,PA,GB cắt nhau tại T . Biết TH = 3 cm,TP=TG=4 cm a, Tính HM,PA,GB. b, Chứng minh tam giác HPG cân

mk pit làm phần a thui
vì AG=2GM
+) AG=4 cm
=>4=2GM
=> MG=4:2=2 (cm)
+)gm+ag=am
+)mg=2 cm
+) ag=9cm
=>2+9=am
=> am=11 cm
tính độ dài đoạn cp và bn tương tự như trên

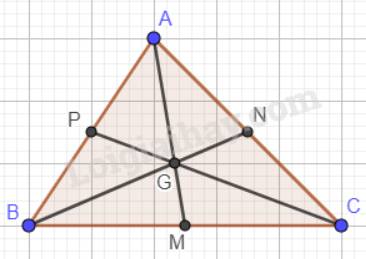
Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài đường trung tuyến đi qua đỉnh ấy nên:
\(\begin{array}{l}\dfrac{{GA}}{{AM}} = \dfrac{{GB}}{{BN}} = \dfrac{{GC}}{{CP}} = \dfrac{2}{3}\\ \to GA = \dfrac{2}{3}AM;GB = \dfrac{2}{3}BN;GC = \dfrac{2}{3}CP\end{array}\)
Vậy:
\(GA + GB + GC = \dfrac{2}{3}AM + \dfrac{2}{3}BN + \dfrac{2}{3}CP = \dfrac{2}{3}(AM + BN + CP)\).

a) Theo bài ra: vuông tại A
áp dụng Định lý Pytago ta có
b)
Trong tam giác vuông ABC có trung tuyến AM nên
AG = ...

Tự vẽ hình
a,AD ĐL py-ta-go vào \(\Delta\)vuông ABC có
\(BC^2=AB^2+AC^2\)
\(x^2=9^2+12^2\)
\(x^2=81+144\)
\(x^2=225\)
\(x=\sqrt{225}=15\)
b,Xét \(\Delta BAN\)và \(\Delta CDN\)có:
BN=DN
\(\widehat{BNA}=\widehat{DNC}\)
NA=NC
\(\Rightarrow\Delta BNA=\Delta CDN\left(c.g.c\right)\)
c,Vì \(\Delta BNA=\Delta CND\left(cmt\right)\)
\(\Rightarrow\widehat{BAN}=\widehat{DCN}\)(2 cạnh t.ư)
Mà 2 góc này ở VTSLT
\(\Rightarrow CD//AB\)


a) Theo bài ra: \(\Delta ABC\) vuông tại A
\(\Rightarrow\)Áp dụng Định lý Pytago ta có :
\(AB^2AC^2=AB^2\rightarrow AB^2=9^2+12^2=BC=\sqrt{255}=\)15(cm)
b)
Trong tam giác vuông ABC có trung tuyến AM nên : AM=BC: 2 =\(\frac{15}{2}\)
\(\rightarrow\)AG = ...

A B C M G N D
a) Xét \(\Delta ABC\) vuông tại A có: \(BC^2=AB^2+AC^2\) (định lí Pytago)
\(\Rightarrow BC^2=225\Rightarrow BC=\sqrt{225}=15\left(cm\right)\)
Vậy \(BC=15cm\).
b) Xét \(\Delta ABC\) vuông tại A có AM là đường trung truyến
\(\Rightarrow AM=\frac{1}{2}BC\) (định lí)
\(\Rightarrow AM=\frac{1}{2}.15=7,5\)
Ta có: 2 đường trung truyến AM và BN cắt nhau tại G
\(\Rightarrow\)G là trọng tâm của \(\Delta ABC\)
\(\Rightarrow AG=\frac{2}{3}AM=\frac{2}{3}.7,5=5\left(cm\right)\)
Vậy \(AG=5cm\).
c) Xét \(\Delta ABN\) và \(\Delta CDN\) có:
BN = DN (gt)
\(\widehat{ANB}=\widehat{CND}\) (2 góc đối đỉnh)
AN = CN (vì N là trung điểm của AC)
\(\Rightarrow\Delta ABN=\Delta CDN\left(c.g.c\right)\) (đpcm)
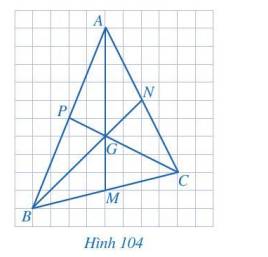
- Ta có: MB = MC và M nằm giữa B và C nên M là trung điểm của BC.
Do đó, AM có là đường trung tuyến của tam giác ABC
- Ta có:
\(\begin{array}{l}\dfrac{{GA}}{{MA}} = \dfrac{6}{9} = \dfrac{2}{3};\\\dfrac{{GB}}{{NB}} = \dfrac{2}{3};\\\dfrac{{GC}}{{PC}} = \dfrac{2}{3}\end{array}\)