Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

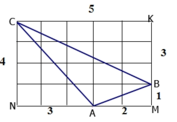
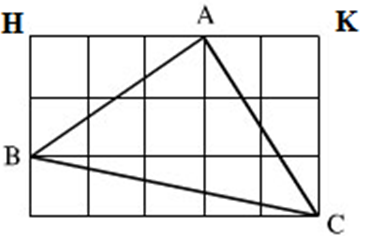
Áp dụng định lí Pi-ta-go trong ΔAMB vuông tại M ta có:
AB2 = AM2 + MB2 = 22 + 12 = 5
⇒ AB = √5
Áp dụng định lí Pi-ta-go trong ΔANC vuông tại N ta có:
AC2 = AN2 + NC2 = 32 + 42 = 25
⇒ AC = 5
Áp dụng định lí Pi-ta-go trong ΔBKC vuông tại K ta có:
BC2 = BK2 + KC2 = 32 + 52 = 34
⇒ BC = √34

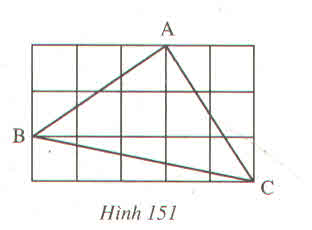
Xét tam giác ABC trên hình vẽ ta có:
AB = AC = 6 ô vuông (với điều kiện tất cả ô vuông đều bằng nhau).
=> Tam giác ABC là tam giác cân và cân tại A.


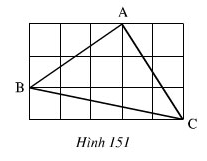
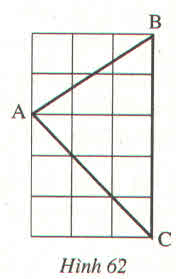
Gọi độ dài cạnh của mỗi ô vuông là 1.
Theo định lí Py-ta-go:
AB2 = 12 + 22 = 1 + 4 = 5
BC2 = 12 + 22 = 1 + 4 = 5
AC2 = 12 + 32 = 1 + 9 = 10
Do AB2 = BC2 nên AB = BC
Do AB2 + BC2 = AC2 nên \(\widehat{ABC}=90^o\)
Vậy \(\Delta ABC\) vuông cân tại B.

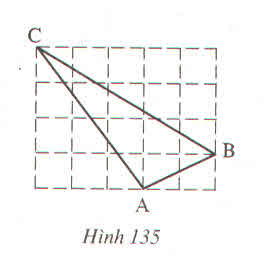
Giả sử độ dài mỗi ô vuông nhỏ là 1
Đường chéo mỗi ô vuông là Căn 2.
Độ dài các cạnh AB, AC, BC lần lượt là: ( căn 13) , 3 căn 2, 5
Ta thấy 3 cạnh không bằng nhau nên không phải tam giác đều.
Thử định lý pytago đảo không đúng nên không phải tam giác vuông.
So sánh tỉ lện giữ cách cạnh đều nhỏ hơn 2. Nên trong tam giác không có góc tù. Vậy tam giác là tam giác nhọn

Gọi mỗi góccòn lại trên giấy ô vuông là K; M; N
Xét Tg AMB vuông tại M ta có:
AB^2 = AM^2 + MB^2 (định lí Pi-ta-go)
Thay số: AB^2 = 22 + 12 = 5
=> AB = căn 5
Xét Tg ANC vuông tại N ta có:
AC^2 = AN^2 + NC^2 (định lí Pi-ta-go )
AC^2= 32 + 42 = 25
=> AC = 5
Xét Tg BKC vuông tại K ta có:
BC^2= BK^2+ KC^2(định lí Pi-ta-go )
BC^2 = 32 + 52 = 34
=>BC= căn 34

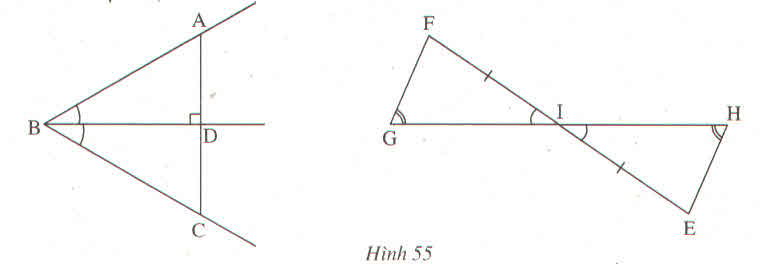
-Xét tam giác vuông BDA và tam giác vuông BDC có:
ABD = CBD
BD: cạnh chung
=> tam giác BDA = tam giác BDC
-Ta có: góc G = góc H
góc FIG = góc EIH
Mà F + G + FIG = E + H + EIH = 1800
=> góc F = góc E
Xét tam giác IFG và tam giác IEH có:
IF = IE (gt)
FIG = EIH (gt)
góc F = góc E (cmt)
=> tam giác IFG = tam giác IEH

Mk hỏi chút xíu: Câu bạn hỏi trong sách pải k? Vậy thì ở sách toán nào thế, trang bao nhiu? Để mk xem, nếu lm đc, mk sẽ giúp bn.


Ta có: AB2=AM2+MB2
=22+12=5
Nên AB= √5
AC2=AN2+NC2
=9+16=52
nên AC=5
BC2=BK2+KC2
= 32+52=9+25=34
BC= √34
Giải:
Ta có: AB2=AM2+MB2
=22+12=5
Nên AB= √5
AC2=AN2+NC2
=9+16=52
nên AC=5
BC2=BK2+KC2
= 32+52=9+25=34
BC= √34