Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

Ta có: điều kiện xác định của bpt \(x+3-\dfrac{1}{x+7}< -\dfrac{1}{x+7}\) là \(x\ne-7\)
\(\Rightarrow x=-7\) không phải là nghiệm của bpt trên
Lại có: \(x+3< 2\\ \Leftrightarrow x< 2-3\\ \Leftrightarrow x< -1\)
\(\Rightarrow x=-7\) thỏa mãn bpt \(x+3< 2\) \(\left(-7< -1\right)\)

Đkxđ: \(\left\{{}\begin{matrix}5-x\ge0\\x-10>0\\\left(x-4\right)\left(x+5\right)\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\le5\\x>10\\x\ne4\\x\ne-5\end{matrix}\right.\)\(\Leftrightarrow x\in\varnothing\).
Vậy BPT vô nghiệm.
Tổng các nghiệm nguyên của bất phương trình \(\dfrac{x-2}{\sqrt{x-4}}\le\dfrac{4}{\sqrt{x-4}}\) bằng

ĐKXĐ: \(x>4\)
\(\dfrac{x-2}{\sqrt{x-4}}\le\dfrac{4}{\sqrt{x-4}}\Rightarrow x-2\le4\)
\(\Rightarrow x\le6\Rightarrow4< x\le6\)
\(\Rightarrow x=\left\{5;6\right\}\Rightarrow5+6=11\)

a)
x^2 +1 >0 mọi x
BPT \(\Leftrightarrow x^2+3x-10< 0\) {\(\Delta=9+40=49\)}
\(\Rightarrow-5< x< 2\)
b)
5+x^2 > 0 với mọi x BPT \(\Leftrightarrow20-2x-x^2-5>0\Leftrightarrow x^2+2x-15< 0\){\(\Delta'=1+15=16\)}
\(\Rightarrow-5< x< 3\)

Cách 1 (đồ thị): Đầu tiên ta xác định miền nghiệm của hệ bất phương trình sau: \(\left\{{}\begin{matrix}x>0\\y>0\\\dfrac{x}{3}+\dfrac{y}{4}\le1\end{matrix}\right.\) như sau:
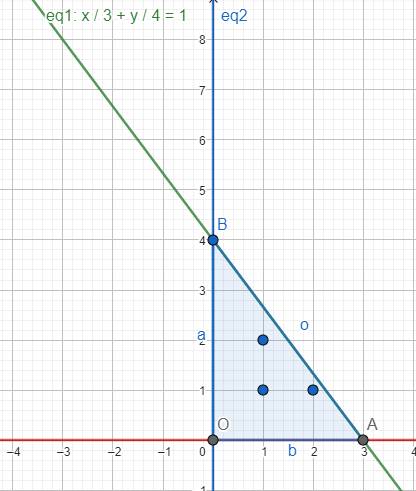
Sau đó ta tìm tất cả các điểm nguyên nằm ở miền trong tam giác OAB. Ta nhận thấy các điểm này là \(\left(1,1\right);\left(1,2\right);\left(2,1\right)\). Vậy các nghiệm (x; y) của bpt là \(\left(1;1\right),\left(1;2\right),\left(2;1\right)\)
Cách 2: (đại số)
Ta có \(\dfrac{x}{3}+\dfrac{y}{4}\le1\) nên \(\dfrac{x}{3}< 1\) \(\Leftrightarrow x< 3\) \(\Rightarrow x\in\left\{1,2\right\}\)
\(\dfrac{y}{4}< 1\Rightarrow y< 4\Rightarrow y\in\left\{1,2,3\right\}\)
Thử lại, ta thấy chỉ có các cặp \(\left(x;y\right)=\left(1;1\right),\left(1;2\right),\left(2;1\right)\) là thỏa mãn. Vậy...

a)
Để \(5x^2-x+m>0\) thì:
\(\Delta< 0\Rightarrow1-20m< 0\Rightarrow m>\dfrac{1}{20}\)
b)
\(mx^2-10x-5< 0\)
Xét \(m=0\) ta có: \(-10x-5< 0\)\(\Leftrightarrow x>\dfrac{1}{2}\) (loại)
Xét \(m\ne0\). Theo định lý về dấu tam thức bậc hai:
\(mx^2-10x-5< 0\)\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\25+5m< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\m< -5\end{matrix}\right.\)\(\Leftrightarrow m< -5\).
Vậy với \(m< -5\) thì \(mx^2-10x-5< 0\).

a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
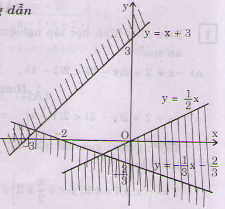
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).
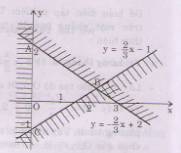
10x2/x2-100 < 10
<=> 10x2/x2-100 - 10 <0
<=> 10x^2 - 10(x^2-100)/x^2 - 100 <0
<=> 1000/x^2-100 <0
<=> x^2 - 100 <0
<=> x^2 <100
<=> 0 <x <10
=> x nguyên dương => x= 1,2,3,...,9
=> tổng các nghiệm nguyên dương của bpt là 1+2+3+...+9=9.10/2 = 45