
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


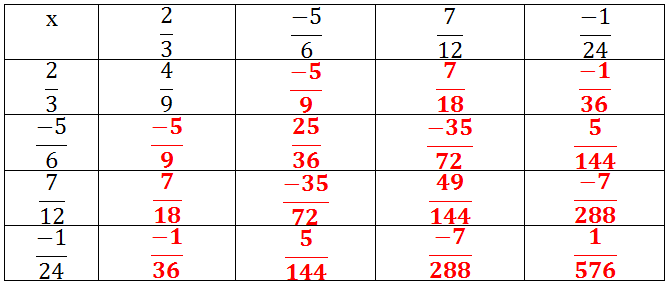
|
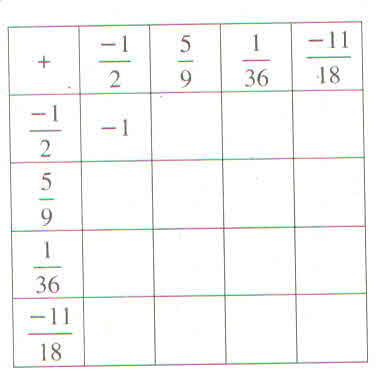
+ |
−12−12 |
5959 |
136136 |
−1118−1118 |
|
−12−12 |
- 1 |
118118 |
−1736−1736 |
−109−109 |
|
5959 |
118118 |
109109 |
712712 |
−118−118 |
|
136136 |
−1736−1736 |
712712 |
118118 |
−712−712 |
|
−1118−1118 |
−109−109 |
−118−118 |
−712−712 |
|
|
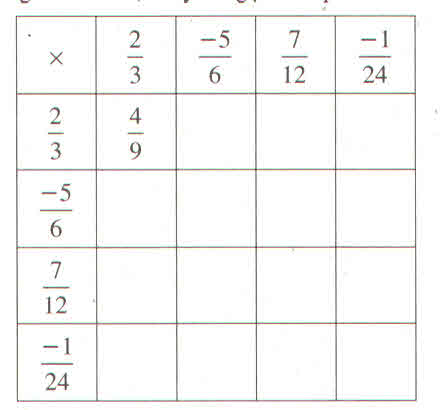
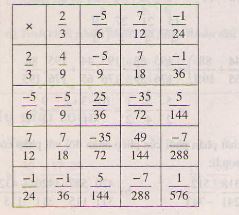
+ |
−12−12 |
5959 |
136136 |
−1118−1118 |
|
−12−12 |
- 1 |
118118 |
−1736−1736 |
−109−109 |
|
5959 |
118118 |
109109 |
712712 |
−118−118 |
|
136136 |
−1736−1736 |
712712 |
118118 |
−712−712 |
|
−1118−1118 |
−109−109 |
−118−118 |
−712−712 |
−119−119 |

Kết quả tìm được đúng
Phương pháp này không thể áp dụng để rút gọn các phân số có dạng \(\dfrac{\overline{ab}}{\overline{bc}}\)
VD: Phân số \(\dfrac{26}{64}\) có dạng \(\dfrac{\overline{ab}}{\overline{bc}}\) nhưng khi rút gọn thì được phân số \(\dfrac{13}{32}\) , chứ không phải phân số \(\dfrac{1}{2}\) theo phương pháp trên ta có được.
Hoặc là phân số \(\dfrac{18}{88}\) có dạng \(\dfrac{\overline{ab}}{\overline{bc}}\) nhưng khi rút gọn thì được phân số \(\dfrac{9}{44}\) , chứ không phải phân số \(\dfrac{1}{8}\) theo phương pháp trên ta có được.
Kiểm tra ta thấy các kết quả tìm được đều đúng. Tuy nhiên, không thể áp dụng "phương pháp" trên để rút gọn các phân số có dạng ab/bc.
Ví dụ :
Cách "rút gọn" của bạn Minh chỉ đúng một cách ngẫu nhiên

Các kết quả trên đều đúng nên mình điền luôn kết quả nha bạn:
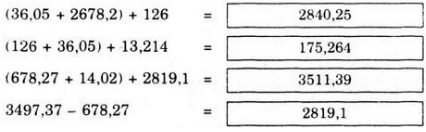
(36,05+2678,2)+126=2840,25.
(126+36,05)+13,214=175,264.
(678,27+14,02)+2819,1=3511,39.
3497,37-678,27=2819,1.
Đó là kết quả của mình có gì sai thì mog pn chỉ ra và giúp mik sửa lỗi nhé!
- Các phép cộng đều cho kết quả đúng.
- Ta có:
(36,05 + 2678,2) + 126
= 36,05 + (2678,2 + 126) (Tính chất kết hợp)
= 36,05 + 2804,2 (theo a)
= 2840,25 (theo c)
(126 + 36,05) + 13,214
= 126 + (36,05 + 13,214) (tính chất kết hợp)
= 126 + 49,264 (theo b)
= 175,264 (theo d)
(678,27 + 14,02) + 2819,1
= (678,27 + 2819,1) + 14,02 (Tính chất giao hoán và kết hợp)
= 3497,37 + 14,02 (theo e)
= 3511,39 (theo g)
3497,37 – 678,27 = 2819,1 (suy từ e)
Vì vậy ta có thể điền số thích hợp và ô trống mà không cần tính toán:


Gọi \(ƯC\left(12n+1;30n+2\right)=d\)
\(\Rightarrow12n+1⋮d\Rightarrow60n+5⋮d\)
và \(30n+2⋮d\Rightarrow60n+ 4⋮d\)
Do đó \(60n+5-60n-4⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=1\)
Vậy \(\dfrac{12n+1}{30n+2}\) là phân số tối giản.
Gọi (12n+1),(30n+2) là d (1)
=>30n+2 \(⋮\) d
=> 2(30n + 2) \(⋮\) d hay 60n +4 \(⋮\) d
Tương tự ta chưng minh:
12n + 1 \(⋮\)d (2)
=> 5(12n+1) \(⋮\) d hay 60n +5 \(⋮\)d
Do đó (60n + 5) - ( 60n +4 ) \(⋮\)d hay 1 \(⋮\) d
=> d = 1 hoặc -1
Từ (1) và(2) ta có( 12n+1 ;30n+2) =1
=> P/s 12n + 1 /30n+2 là ps tối giản
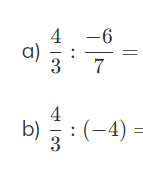


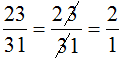




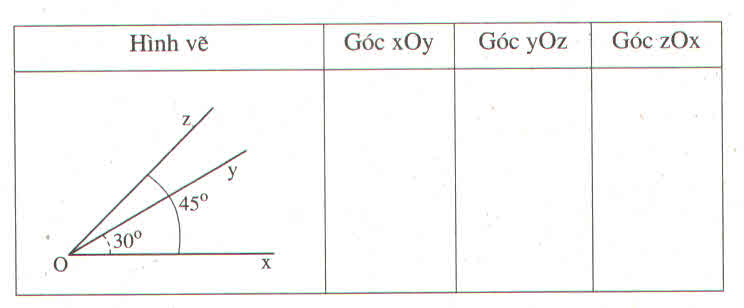
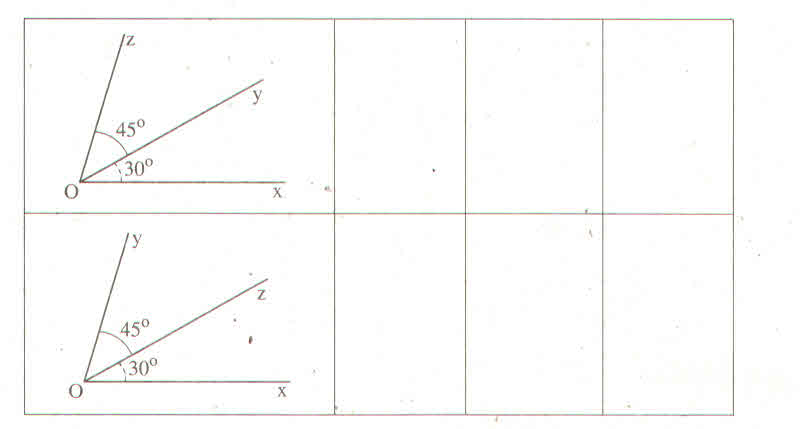
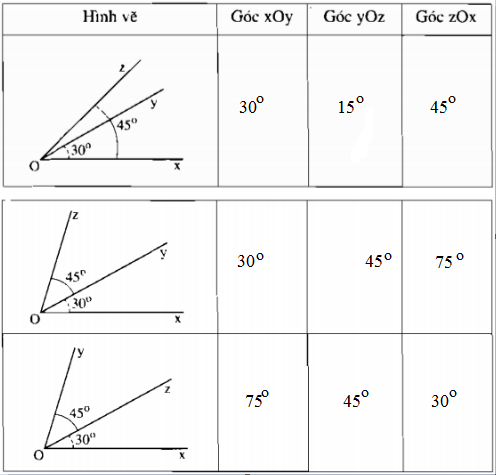
\(\dfrac{4\times7}{3\times\left(-6\right)}=\dfrac{2\times7}{3\times\left(-3\right)}=\dfrac{14}{-9}=\dfrac{14}{9}\)
\(\dfrac{4}{3\times-4}=\dfrac{1}{-3}=\dfrac{1}{3}\)