Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đặt bt trên là A
\(\frac{1}{2}\)A=\(\frac{3}{15.18}+\frac{3}{18.21}+\frac{3}{21.24}+...+\frac{3}{87.90}\)
\(\frac{1}{2}\)A=\(\frac{1}{15}-\frac{1}{18}+\frac{1}{18}-\frac{1}{21}+\frac{1}{21}-....+\frac{1}{87}-\frac{1}{90}\)
\(\frac{1}{2}A=\frac{1}{15}-\frac{1}{90}\)
..... tự tính nhé

B=5/18*21+5/21*24+5/24*27+...+5/123*126
3/5B=3/5(5/18*21+5/21*24+...+5/123*126)
3/5B=3/5*5/18*21+3/5*5/21*24+...+3/5*5/123*126
3/5B=3/18*21+3/21*24+...+3/123*126
3/5B=1/18-1/21+1/21-1/24+...+1/123-1/126
3/5B=1/18-1/126
3/5B=126/2268-18/2268
3/5B=108/2268
3/5B=21
B=21÷3/5
B=21*5/3
B=35

a) A = 1/3 - 1/7 + 1/7 - 1/11 +......+1/107 - 1/111
A = 1/3 - 1/111
A = ..............Bạn tự tính nhé!
b) B = 2.(3/15.18 + 3/18.21 +........+3/87.90)
B = 2.(1/15 - 1/18 + 1/18 - 1/21 +........+1/87 - 1/90)
B = 2.(1/15 - 1/90)
B = 2.5/90
B =......Tự tính nhé!
C ; D làm tương tự nhé!

\(A=2\left(\frac{1}{15}-\frac{1}{18}+\frac{1}{18}-\frac{1}{21}+......+\frac{1}{87}-\frac{1}{90}\right)\)
\(\Rightarrow A=2\left(\frac{1}{15}-\frac{1}{90}\right)\)
\(\Rightarrow A=2.\frac{1}{18}=\frac{1}{9}\)
\(A=\frac{6}{15.18}+\frac{6}{18.21}+\frac{6}{21.24}+...+\frac{6}{87.90}\)
\(=6.\frac{1}{3}.\left(\frac{3}{15.18}+\frac{3}{18.21}+\frac{3}{21.24}+...+\frac{3}{87.90}\right)\)
\(=2.\left(\frac{1}{15}-\frac{1}{18}+\frac{1}{18}-\frac{1}{21}+\frac{1}{21}-\frac{1}{24}+...+\frac{1}{87}-\frac{1}{90}\right)\)
\(=2.\left(\frac{1}{15}-\frac{1}{90}\right)\)
\(=2.\frac{1}{18}\)
\(=\frac{1}{9}\)
\(B=\frac{1}{10}+\frac{1}{15}+\frac{1}{21}+...+\frac{1}{120}\)
\(=\frac{2}{20}+\frac{2}{30}+\frac{2}{42}+...+\frac{2}{240}\)
\(=\frac{2}{4.5}+\frac{2}{5.6}+\frac{2}{5.7}+...+\frac{2}{15.16}\)
\(=2.\left(\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+...+\frac{1}{15.16}\right)\)
\(=2.\left(\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+...+\frac{1}{15}-\frac{1}{16}\right)\)
\(=2.\left(\frac{1}{4}-\frac{1}{16}\right)\)
\(=2.\frac{3}{16}\)
\(=\frac{3}{8}\)

Tính các tổng dưới đây sau khi đã rút gọn phân số :
a)\(\dfrac{7}{21}\) + \(\dfrac{9}{-36}\) = \(\dfrac{7}{21}\)+\(\dfrac{-9}{36}\)=\(\dfrac{1}{3}\)+\(\dfrac{-1}{4}\)=\(\dfrac{4}{12}\)+\(\dfrac{-3}{12}\)=\(\dfrac{1}{12}\)
b) \(\dfrac{-12}{18}\)+\(\dfrac{-21}{35}\)=\(\dfrac{-2}{3}\)+\(\dfrac{-3}{5}\)=\(\dfrac{-10}{15}\)+\(\dfrac{-9}{15}\)=\(\dfrac{-19}{15}\)
c) \(\dfrac{-3}{21}\)+\(\dfrac{6}{42}\)=\(\dfrac{-1}{7}\)+\(\dfrac{1}{7}\)=0
d) \(\dfrac{-18}{24}\)+\(\dfrac{15}{-21}\)=\(\dfrac{-18}{24}\)+\(\dfrac{-15}{21}\)=\(\dfrac{-3}{4}\)+\(\dfrac{-5}{7}\)=\(\dfrac{-21}{28}\)+\(\dfrac{-20}{28}\)=\(\dfrac{-41}{28}\)

b, \(K =\) \(\dfrac{75}{100}+\dfrac{18}{21}+\dfrac{19}{32}+\dfrac{1}{4}+\dfrac{3}{21}+\dfrac{13}{32}\)
\(K = \) \(\dfrac{3}{4}+\dfrac{18}{21}+\dfrac{19}{32}+\dfrac{1}{4}+\dfrac{3}{21}+\dfrac{13}{32}\)
\(K = \) \(\left(\dfrac{3}{4}+\dfrac{1}{4}\right)+\left(\dfrac{18}{21}+\dfrac{3}{21}\right)+\left(\dfrac{19}{32}+\dfrac{13}{32}\right)\)
\(K = \) \(1 + 1 + 1\)
\(K = \) \(3\)

1.a) Dễ nhận thấy đề toán chỉ giải được khi đề là tìm x,y. Còn nếu là tìm x ta nhận thấy ngay vô nghiệm. Do đó: Sửa đề: \(\left|x-3\right|+\left|2-y\right|=0\)
\(\Leftrightarrow\left|x-3\right|=\left|2-y\right|=0\)
\(\left|x-3\right|=0\Rightarrow\left\{{}\begin{matrix}x-3=0\\-\left(x-3\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\) (1)
\(\left|2-y\right|=0\Rightarrow\left\{{}\begin{matrix}2-y=0\\-\left(2-y\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\y=-2\end{matrix}\right.\) (2)
Từ (1) và (2) có: \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x_1=3\\x_2=-3\end{matrix}\right.\\\left\{{}\begin{matrix}y_1=2\\y_2=-2\end{matrix}\right.\end{matrix}\right.\)

\(\dfrac{7}{21}+\dfrac{-9}{36}=\dfrac{1}{3}+\dfrac{-1}{4}=\dfrac{4}{12}+\dfrac{-3}{12}=\dfrac{1}{12}\)
\(\dfrac{-12}{18}+\dfrac{-21}{35}=\dfrac{-2}{3}+\dfrac{-3}{5}=\dfrac{-10}{15}+\dfrac{-9}{15}=\dfrac{-19}{15}\)
\(\dfrac{-18}{14}+\dfrac{15}{-21}=\dfrac{-9}{7}+\dfrac{-5}{7}=\dfrac{-14}{7}=-2\)
\(\dfrac{3}{21}+\dfrac{-6}{42}=\dfrac{1}{7}+\dfrac{-1}{7}=0\)

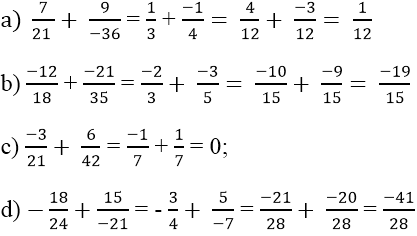
Theo đề bài, ta có:
A = \(\dfrac{6}{15.18}+\dfrac{6}{18.21}+\dfrac{6}{21.24}+...+\dfrac{6}{87.90}\)
A = \(2.\left(\dfrac{3}{15.18}+\dfrac{3}{18.21}+\dfrac{3}{21.24}+...+\dfrac{3}{87.90}\right)\)
A =\(2.\left(\dfrac{1}{15}-\dfrac{1}{18}+\dfrac{1}{18}-\dfrac{1}{21}+\dfrac{1}{21}-\dfrac{1}{24}+...+\dfrac{1}{87}-\dfrac{1}{90}\right)\)
A = \(2.\left(\dfrac{1}{15}-\dfrac{1}{90}\right)\)= \(\dfrac{1}{8}\)
A= \(\dfrac{6}{15.18}+\dfrac{6}{18.21}+...+\dfrac{6}{87.90}\)
A= \(2\left(\dfrac{3}{15.18}+\dfrac{3}{18.21}+...+\dfrac{3}{87.90}\right)\)
A= \(2\left(\dfrac{1}{15}-\dfrac{1}{18}+\dfrac{1}{18}-\dfrac{1}{21}+...+\dfrac{1}{87}-\dfrac{1}{90}\right)\)
A= \(2\left(\dfrac{1}{15}-\dfrac{1}{90}\right)\)
A= 2. \(\dfrac{1}{16}\)
A= \(\dfrac{1}{8}\)