Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chứng minh các biểu thức đã cho không phụ thuộc vào x.
Từ đó suy ra f'(x)=0
a) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
b) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
c) f(x)=\(\frac{1}{4}\)(\(\sqrt{2}\)-\(\sqrt{6}\))=>f'(x)=0
d,f(x)=\(\frac{3}{2}\)=>f'(x)=0

a) f'(x) = - 3sinx + 4cosx + 5. Do đó
f'(x) = 0 <=> - 3sinx + 4cosx + 5 = 0 <=> 3sinx - 4cosx = 5
<=> sinx -
cosx = 1. (1)
Đặt cos φ = , (φ ∈
) => sin φ =
, ta có:
(1) <=> sinx.cos φ - cosx.sin φ = 1 <=> sin(x - φ) = 1
<=> x - φ = + k2π <=> x = φ +
+ k2π, k ∈ Z.
b) f'(x) = - cos(π + x) - sin = cosx + sin
.
f'(x) = 0 <=> cosx + sin = 0 <=> sin
= - cosx <=> sin
= sin
<=> =
+ k2π hoặc
= π - x +
+ k2π
<=> x = π - k4π hoặc x = π + k, (k ∈ Z).

Theo định nghĩa ta có :
\(f'\left(x\right)=\lim\limits_{\Delta x\rightarrow0}\frac{f\left(a+\right)-f\left(a\right)}{\Delta x}\)
\(=\lim\limits_{\Delta x\rightarrow0}\frac{\left(a+\Delta x-1\right)\varphi\left(a+\Delta x\right)}{\Delta x}\) do (\(f\left(a\right)=0\))
\(=\lim\limits_{\Delta x\rightarrow0}\varphi\left(a+\Delta x\right)\)
Khi \(\Delta x\rightarrow0\) thì \(a+\Delta x\rightarrow a\) và do \(\varphi\left(x\right)\) là hàm liên tục tại x = a nên có :
\(\lim\limits_{\Delta x\rightarrow0}\varphi\left(a+\Delta x\right)=\varphi\left(a\right)\)
Vậy \(f'\left(a\right)=\varphi\left(a\right)\)

Lời giải:
Ta có:
\(f(x)=\sin ^2\left(\frac{\pi}{6}-x\right)+\sin ^2\left(\frac{\pi}{6}+x\right)\)
\(\Rightarrow f'(x)=2\sin \left(\frac{\pi}{6}-x\right).-\cos \left(\frac{\pi}{6}-x\right)+2\sin \left(\frac{\pi}{6}+x\right)\cos \left(\frac{\pi}{6}+x\right)\)
\(f'(x)=-\sin 2\left(\frac{\pi}{6}-x\right)+\sin 2\left(\frac{\pi}{6}+x\right)\)
Áp dụng công thức: \(\sin a-\sin b=2\cos \frac{a+b}{2}\sin \frac{a-b}{2}\) suy ra:
\(f'(x)=-\sin \left(\frac{\pi}{3}-2x\right)+\sin \left(\frac{\pi}{3}+2x\right)\)
\(f'(x)=2\cos \left(\frac{\pi}{3}\right)\sin 2x=\sin 2x\) (đpcm)
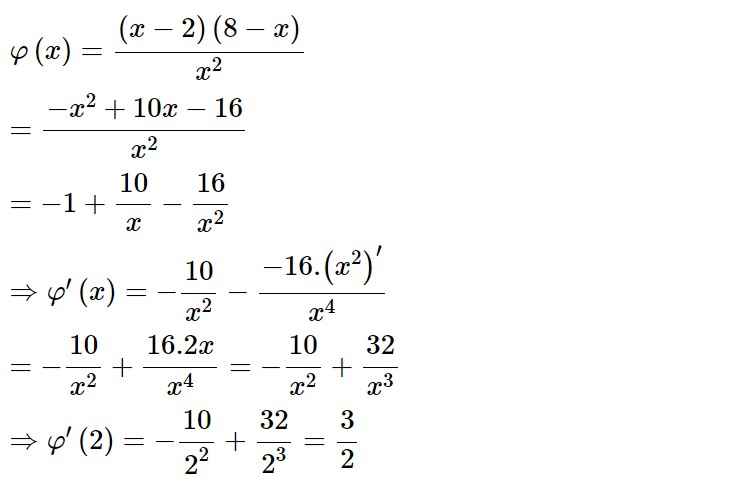
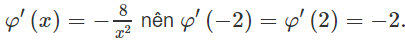
Ta có f'(x) = 2x, suy ra f'(1) = 2
và φ'(x) = 4 +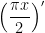 . cos
. cos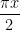 = 4 +
= 4 + 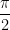 . cos
. cos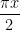 , suy ra φ'(1) = 4.
, suy ra φ'(1) = 4.
Vậy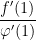 =
=  =
=  .
.