Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt 3759=a; 5741=b
Theo đề, ta có: \(E=4\dfrac{7}{b}\cdot\dfrac{1}{a}-\dfrac{4}{a}\cdot\left(1+\dfrac{2}{b}\right)+\dfrac{1}{a}+\dfrac{1}{ab}\)
\(=\dfrac{4b+7}{b}\cdot\dfrac{1}{a}-\dfrac{4}{a}\cdot\dfrac{b+2}{b}+\dfrac{b+1}{ab}\)
\(=\dfrac{4b+7-4b-8+b+1}{ab}=\dfrac{b}{ab}=\dfrac{1}{a}=\dfrac{1}{3759}\)

\(xy\left(x-y\right)+yz\left(y-z\right)+xz\left(z-x\right)\\ =xy\left(x-y\right)+yz\left[-\left(x-y\right)-\left(z-x\right)\right]+xz\left(z-x\right)\\ =xy\left(x-y\right)-yz\left(x-y\right)-yz\left(z-x\right)+xz\left(z-x\right)\\ =\left(x-y\right)\left(xy-yz\right)+\left(z-x\right)\left(xz-yz\right)\\ =y\left(x-y\right)\left(x-z\right)+z\left(z-x\right)\left(x-y\right)\\ =\left(x-y\right)\left(x-z\right)\left(y-z\right)\)


a)Nhận xét
\(\dfrac{n^3+1}{n^3-1}=\dfrac{\left(n+1\right)\left(n^2-n+1\right)}{\left(n-1\right)\left(n^2+n+1\right)}=\dfrac{\left(n+1\right)\left[\left(n-0,5\right)^2+0;75\right]}{\left(n-1\right)\left[\left(n+0,5\right)^2+0,75\right]}\)
Áp dụng công thức trên:
\(A=\dfrac{2^3+1}{2^3-1}.\dfrac{3^3+1}{3^3-1}....\dfrac{9^3+1}{9^3-1}\)
\(=\dfrac{\left(2+1\right)\left[\left(2-0,5\right)^2+0,75\right]}{\left(2-1\right)\left[\left(2+0,5\right)^2+0,75\right]}.\dfrac{\left(3+1\right)\left[\left(3-0,5\right)^2+0,75\right]}{\left(3-1\right)\left[\left(3+0,5\right)^2+0,75\right]}...\dfrac{\left(9+1\right)\left[\left(9-0,5\right)^2+0,75\right]}{\left(9-1\right)\left[\left(9+0,5\right)^2+0,75\right]}\)
\(=\dfrac{3\left(1,5^2+0,75\right)}{\left(2,5^2+0,75\right)}.\dfrac{4\left(2,5^2+0,75\right)}{2\left(3,5^2+0,75\right)}...\dfrac{10\left(8,5^2+0,75\right)}{8\left(9,5^2+0,75\right)}\)
\(=\dfrac{3.4....10}{1.2.....8}.\dfrac{1,5^2+0,75}{9,5^2+0,75}\)
\(=\dfrac{9.10}{2}.\dfrac{3}{91}\)
\(=\dfrac{3}{2}.\dfrac{90}{91}< \dfrac{3}{2}\)
\(\Rightarrowđpcm\)
b) Làm tương tự

1, \(A=\dfrac{-2}{4}+\dfrac{2}{7}-\dfrac{5}{28}\)
\(A=\dfrac{-1}{2}+\dfrac{2}{7}-\dfrac{5}{28}\)
\(A=\dfrac{-14+8-5}{28}=\dfrac{-11}{28}\)
2, \(B=\left(\dfrac{5}{7}.0,6-5:3\dfrac{1}{2}\right).\left(40\%-1,4\right).\left(-2\right)^3\)
\(B=\dfrac{-13}{14}.\left(-1\right).8=\dfrac{52}{7}\)
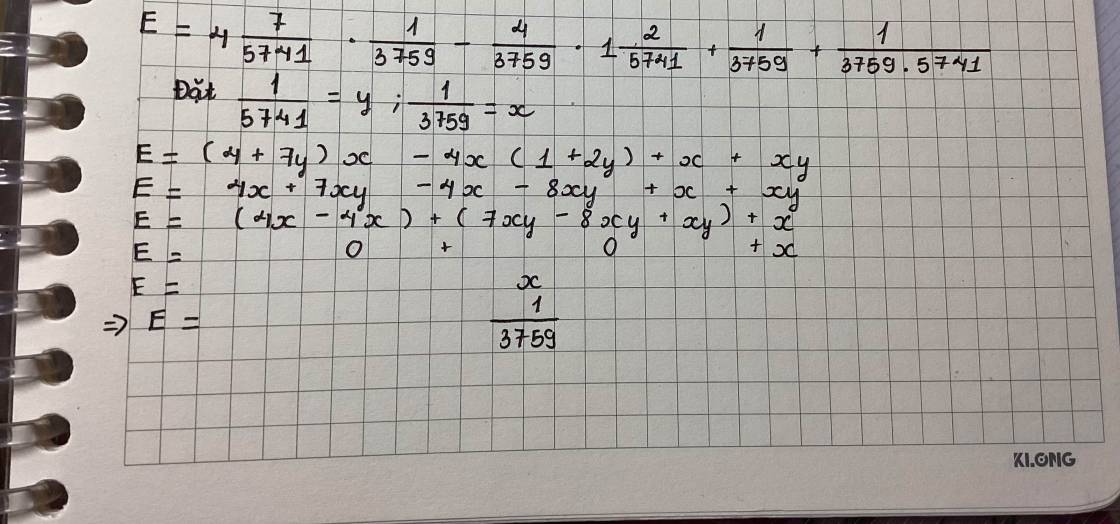
\(4\dfrac{7}{5741}\cdot\dfrac{1}{3759}-\dfrac{4}{3759}\cdot1\dfrac{2}{5741}+\dfrac{1}{3759}+\dfrac{1}{3759\cdot5741}\\ =\dfrac{22971}{5741}\cdot\dfrac{1}{3759}-\dfrac{1}{3759}\cdot\dfrac{22972}{5741}+\dfrac{1}{3759}\cdot\dfrac{5741}{5741}+\dfrac{1}{3759}\cdot\dfrac{1}{5741}\\ =\dfrac{1}{3759}\cdot\left(\dfrac{22971}{5741}-\dfrac{22972}{5741}+\dfrac{5741}{5741}+\dfrac{1}{5741}\right)\\ =\dfrac{1}{3759}\cdot\dfrac{5741}{5741}=\dfrac{1}{3759}\cdot1=\dfrac{1}{3759}\)