Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


th1 : ta có : \(A=2017\left|x-2017\right|+\left|x-2018\right|\)
\(2017\left|x-2017\right|=A-\left|x-2018\right|\ge0\)
\(\Leftrightarrow A\ge\left|x-2018\right|\) dấu "=" xảy ra khi \(x=2017\) khi đó \(A=1\) (1)
th2 : ta có : \(A=2017\left|x-2017\right|+\left|x-2018\right|\)
\(\left|x-2018\right|=A-2017\left|x-2017\right|\ge0\)\(\Leftrightarrow A\ge2017\left|x-2017\right|\) dấu "=" xảy ra khi \(x=2018\) khi đó \(A=2017\) (2)
từ (1) và (2) ta có : giá trị nhỏ nhất của biểu thức \(A\) là \(1\) khi \(x=2017\)

Câu 1:
Để ý rằng \((2-\sqrt{3})(2+\sqrt{3})=1\) nên nếu đặt
\(\sqrt{2+\sqrt{3}}=a\Rightarrow \sqrt{2-\sqrt{3}}=\frac{1}{a}\)
PT đã cho tương đương với:
\(ma^x+\frac{1}{a^x}=4\)
\(\Leftrightarrow ma^{2x}-4a^x+1=0\) (*)
Để pt có hai nghiệm phân biệt \(x_1,x_2\) thì pt trên phải có dạng pt bậc 2, tức m khác 0
\(\Delta'=4-m>0\Leftrightarrow m< 4\)
Áp dụng hệ thức Viete, với $x_1,x_2$ là hai nghiệm của pt (*)
\(\left\{\begin{matrix} a^{x_1}+a^{x_2}=\frac{4}{m}\\ a^{x_1}.a^{x_2}=\frac{1}{m}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a^{x_2}(a^{x_1-x_2}+1)=\frac{4}{m}\\ a^{x_1+x_2}=\frac{1}{m}(1)\end{matrix}\right.\)
Thay \(x_1-x_2=\log_{2+\sqrt{3}}3=\log_{a^2}3\) :
\(\Rightarrow a^{x_2}(a^{\log_{a^2}3}+1)=\frac{4}{m}\)
\(\Leftrightarrow a^{x_2}(\sqrt{3}+1)=\frac{4}{m}\Rightarrow a^{x_2}=\frac{4}{m(\sqrt{3}+1)}\) (2)
\(a^{x_1}=a^{\log_{a^2}3+x_2}=a^{x_2}.a^{\log_{a^2}3}=a^{x_2}.\sqrt{3}\)
\(\Rightarrow a^{x_1}=\frac{4\sqrt{3}}{m(\sqrt{3}+1)}\) (3)
Từ \((1),(2),(3)\Rightarrow \frac{4}{m(\sqrt{3}+1)}.\frac{4\sqrt{3}}{m(\sqrt{3}+1)}=\frac{1}{m}\)
\(\Leftrightarrow \frac{16\sqrt{3}}{m^2(\sqrt{3}+1)^2}=\frac{1}{m}\)
\(\Leftrightarrow m=\frac{16\sqrt{3}}{(\sqrt{3}+1)^2}=-24+16\sqrt{3}\) (thỏa mãn)
Câu 2:
Nếu \(1> x>0\)
\(2017^{x^3}>2017^0\Leftrightarrow 2017^{x^3}>1\)
\(0< x< 1\Rightarrow \frac{1}{x^5}>1\)
\(\Rightarrow 2017^{\frac{1}{x^5}}> 2017^1\Leftrightarrow 2017^{\frac{1}{x^5}}>2017\)
\(\Rightarrow 2017^{x^3}+2017^{\frac{1}{x^5}}> 1+2017=2018\) (đpcm)
Nếu \(x>1\)
\(2017^{x^3}> 2017^{1}\Leftrightarrow 2017^{x^3}>2017 \)
\(\frac{1}{x^5}>0\Rightarrow 2017^{\frac{1}{x^5}}>2017^0\Leftrightarrow 2017^{\frac{1}{5}}>1\)
\(\Rightarrow 2017^{x^3}+2017^{\frac{1}{x^5}}>2018\) (đpcm)

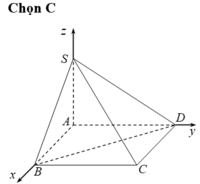
Đặt hệ trục tọa độ Oxyz như hình vẽ.
Khi đó, ta có A (0;0;0), B (a;0;0), D (0; a√3 ; 0), S (0;0;a).
Ta có ![]() , nên đường thẳng BD có vectơ chỉ phương là
, nên đường thẳng BD có vectơ chỉ phương là ![]() .
.
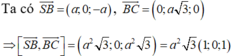
Như vậy, mặt phẳng (SBC) có vectơ pháp tuyến là ![]()
Do đó, α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) thì
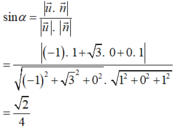

Đáp án A
Phương pháp:
![]()
![]()
![]()
lần lượt là các VTPT. Khi đó, góc giữa hai mặt phẳng α , β được tính
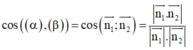
![]()
Cách giải:
(P): x+2y-2z+2018=0
![]()
(Q): x+my+(m-1)z+2017=0
![]()
Góc giữa hai mặt phẳng (P) và (Q):



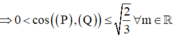
![]()
![]()

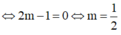
Khi đó

![]()
Ta thấy:
![]()
![]()