Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow\)\(a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow\)\(\left(a+b\right)^3-3ab\left(a+b\right)+c^3-3abc=0\)
\(\Leftrightarrow\)\(\left(a+b\right)^3+c^3-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\)\(\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\)\(\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2-3ab\right]=0\)
Do \(a+b+c\ne0\) nên \(\left(a+b\right)^2-c\left(a+b\right)+c^2-3ab=0\)
\(\Leftrightarrow\)\(a^2+b^2+c^2-ab-bc-ca=0\)
\(\Leftrightarrow\)\(2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)
\(\Leftrightarrow\)\(\left(a^2-2ab+b^2\right)+\left(b^2-bc+c^2\right)+\left(c^2-ca+a^2\right)=0\)
\(\Leftrightarrow\)\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Leftrightarrow\)\(\hept{\begin{cases}a=b\\b=c\\c=a\end{cases}\Leftrightarrow a=b=c}\)
\(\Rightarrow\)\(N=\frac{a^2+b^2+c^2}{\left(a+b+c\right)^2}=\frac{3a^2}{\left(3a\right)^2}=\frac{3a^2}{9a^2}=\frac{1}{3}\)
...

\(.\)M= bn ghi lại đề nha ^.^
\(=\left(a+b\right)^3-3ab\left(a+b\right)+3ab\left[\left(a^2+2ab+b^2\right)-2ab\right]+6a^2b^2\left(a+b\right)\)
\(=1^3-3ab.1+3ab\left[\left(a+b\right)^2-2ab\right]+6a^2b^2.1\)
\(=1-3ab+3ab\left(1-2ab\right)+6a^2b^2\)
\(M=1-3ab+3ab-6a^2b^2+6a^2b^2\)\(=1\)
k cho mình nha bn thanks nhìu <3 <3 (^3^)
2. \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)-24\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\)(1)
Đặt \(x^2+5x+4=t\)
(1) = \(t.\left(t+2\right)-24\)
\(=t^2+2t+1-25\)
\(=\left(t+1\right)^2-25\)
\(=\left(t+1-5\right)\left(t+1+5\right)\)
\(=\left(t-4\right)\left(t+6\right)\)(2)
Thay \(t=x^2+5x+4\)vào (2) ta có:
(2) = \(\left(x^2+5x+4-4\right)\left(x^2+5x+4+6\right)\)
\(=\left(x^2+5x\right)\left(x^2+5x+10\right)\)\(=x\left(x+5\right)\left(x^2+5x+10\right)\)
k mình nha bn <3 thanks

b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)

\(=\left(a+b\right)\left(a^2-ab+b^2\right)+3ab[\left(a+b\right)^2-2ab]+6a^2b^2\left(a+b\right)\)
\(=\left(a+b\right)[\left(a+b\right)^2-3ab]+3ab[\left(a+b\right)^2-2ab+6a^2b^2\left(a+b\right)\)
\(=1-ab+3ab\left(1-2ab\right)+6a^2b^2\)
\(=1-3ab+3ab-6a^2b^2+6a^2b^2\)
\(=1\)
ta có : M=2.(a^3 +b^3) -3.(a^2 + b^2)
<=>M=2.(a+b)(a^2 -ab +b^2) - 3(a^2 +3b^2)
<=>M=2(a^2 -ab +b^2) -3(a^2 +b^2) vì a+b=1(gt)
<=>M=-(a^2 +b^2 +2ab)
<=>M=-(a+b)^2
<=>M=-1 (vì a+b=1)

M=\(a^3+b^3+3ab\left(a^2+b^2\right)+6a^2b^2\left(a+b\right)\)
=\(\left(a+b\right)\left(a^2-ab+b^2\right)-6a^2b^2\left(a+b\right)+6a^2b^2\left(a+b\right)\)
=\(a^2-ab+b^2\)
=\(\left(a+b\right)^2-2ab-ab\)
=-3ab
ta có : M=2.(a^3 +b^3) -3.(a^2 + b^2)
<=>M=2.(a+b)(a^2 -ab +b^2) - 3(a^2 +3b^2)
<=>M=2(a^2 -ab +b^2) -3(a^2 +b^2) vì a+b=1(gt)
<=>M=-(a^2 +b^2 +2ab)
<=>M=-(a+b)^2
<=>M=-1 (vì a+b=1)

\(M=2\left(a^3+b^3\right)-3\left(a^2+b^2\right)\)
\(=2\left(a+b\right)\left(a^2-ab+b^2\right)-3a^2-3b^2\)
\(=2\left(a^2-ab+b^2\right)-3a^2-3b^2\)
\(=2a^2-2ab+2b^2-3a^2-3b^2\)
\(=-a^2-2ab-b^2\)
\(=-\left(a+b\right)^2\)
\(=-1\)
Vậy giá trụ của biểu thức M là - 1 tại a + b = 1
ta có : M=2.(a^3 +b^3) -3.(a^2 + b^2)
<=>M=2.(a+b)(a^2 -ab +b^2) - 3(a^2 +3b^2)
<=>M=2(a^2 -ab +b^2) -3(a^2 +b^2) vì a+b=1(gt)
<=>M=-(a^2 +b^2 +2ab)
<=>M=-(a+b)^2
<=>M=-1 (vì a+b=1)

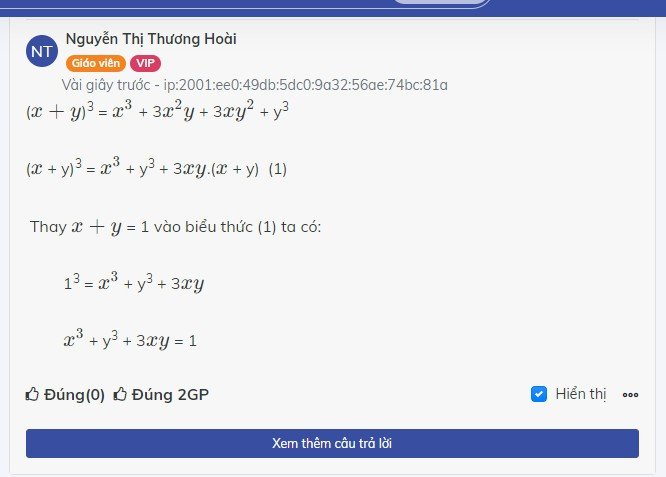
1, \(A=x^3+y^3+3xy\)
\(=x^3+3x^2y+3xy^2+y^2+3xy-3x^2y-3xy^2\)
\(=\left(x+y\right)^3+3xy-3xy\left(x+y\right)\)
Thay x +1 = 1 ta có
\(1^3+3xy-3xy.1=1+3xy-3xy=1\)

a) \(A=1+8+8^2+8^3+....+8^7\)
\(\Rightarrow8A=8+8^2+8^3+8^4+....+8^8\)
\(\Rightarrow8A-A=8^8-1\)
\(\Rightarrow A=\frac{8^8-1}{7}\)
Các bạn có thể tính cụ thể ra vì đây là số nhỏ nhưng đối vs những bài số to thì các bạn chỉ cần làm đến đây thôi
Vậy............
b) \(B=\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\)
\(=\left(3^2+1\right)\left(9^2+1\right)\left(81^2+1\right)\)
\(\Rightarrow\left(3^2-1\right)B=\left(3^2-1\right)\left(3^2+1\right)\left(9^2+1\right)\left(81^2+1\right)\)
\(\Rightarrow8B=\left(9^2-1\right)\left(9^2+1\right)\left(81^2+1\right)\)
\(\Rightarrow8B=\left(81^2-1\right)\left(81^2+1\right)\)
\(\Rightarrow8B=\left(81^4-1\right)\)
\(\Rightarrow B=\frac{81^4-1}{8}\)
Vậy...........
\(A=\dfrac{298^3+48^3}{346}-298\cdot48\)
\(=298^2-2\cdot298\cdot48+48^2\)
\(=250^2=62500\)